题目内容
【题目】在平面直角坐标系中， 
的三个顶点坐标分别为A（2，-4），B（3，-2）， C（6，-3）
①画出△ABC关于
x轴对称的△A1B1C1；
②以M点为位似中心，在网格中画出△A1B1C1的位似图形△A2B2C2 ， 使△A2B2C2与△A1B1C1的相似比为2：1．
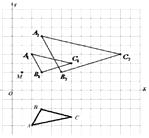
【答案】解：先把A，B，C点关于x轴对称的三点坐标写出来，再描点连线，关于x轴对称的点，横坐标不变，纵坐标互为相反数，
所以A1（2，4），B1（3，2），C1（6，3），在网格中描点连线．
因为位似比为2，所以A2（3，6），B2（5，2），C2（11，4），
在网格中描点连线，如图所示：
【解析】①先根据关于x轴对称点的坐标特点，横坐标不变，纵坐标互为相反数，求出点A1、B1、C1的坐标，再画出△A1B1C1即可。
②根据位似比求出A2，B2，C2的坐标，再连线画出图形即可。
【考点精析】关于本题考查的作轴对称图形和作图-位似变换，需要了解画对称轴图形的方法：①标出关键点②数方格，标出对称点③依次连线；对应点到位似中心的距离比就是位似比，对应线段的比等于位似比，位似比也有顺序；已知图形的位似图形有两个，在位似中心的两侧各有一个．位似中心，位似比是它的两要素才能得出正确答案．
练习册系列答案
相关题目
