ЬтФПФкШн
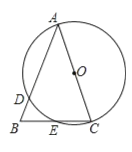
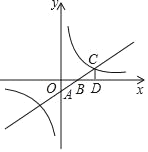
ЁОЬтФПЁПШчЭМ1ЃЌжБЯпABгыxжсЁЂyжсЗжБ№НЛгкЕуAЁЂBЃЌзїЕШбќжБНЧШ§НЧаЮABCЃЌЪЙЁЯBACЃН90ЁуЃЌНЋЁїABCбизХЩфЯпABЦНвЦЕУЕНЁїAЁфBЁфCЁфЃЌЕБЕуAЁфгыЕуBжиКЯЪБЭЃжЙдЫЖЏЃЎЩшЦНвЦОрРыЮЊmЃЌЁїAЁфBЁфCЁфгыЁїABOжиКЯВПЗжЕФУцЛ§ЮЊSЃЌSЙигкmЕФКЏЪ§ЭМЯѓШчЭМ2ЫљЪОЃЎЃЈЦфжа0ЁмmЁм![]() ЪБЃЌКЏЪ§ЕФНтЮіЪНВЛЭЌЃЉ
ЪБЃЌКЏЪ§ЕФНтЮіЪНВЛЭЌЃЉ
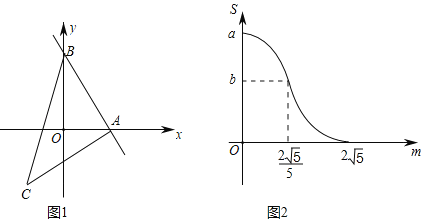
ЃЈ1ЃЉЬюПеЃКaЃНЁЁ ЁЁЃЛ
ЃЈ2ЃЉЧѓжБЯпABЕФНтЮіЪНЃЛ
ЃЈ3ЃЉЧѓSЙигкmЕФНтЮіЪНЃЌВЂаДГіmЕФШЁжЕЗЖЮЇЃЎ
ЁОД№АИЁПЃЈ1ЃЉ10ЃЛЃЈ2ЃЉyЃНЉ![]() x+4ЃЛЃЈ3ЃЉSЃН
x+4ЃЛЃЈ3ЃЉSЃН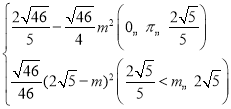 ЃЎ
ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнЭМаЮЦНвЦОрРыm=AB=![]() ЃЌЕБm=0ЪБЭМЯѓЕФУцЛ§МДЪЧШ§НЧаЮABCЕФУцЛ§ЃЌгЩДЫМДПЩЧѓГіaЕФжЕЃЛ
ЃЌЕБm=0ЪБЭМЯѓЕФУцЛ§МДЪЧШ§НЧаЮABCЕФУцЛ§ЃЌгЩДЫМДПЩЧѓГіaЕФжЕЃЛ
ЃЈ2ЃЉИљОнКЏЪ§ЭМЯѓЗЂЩњБфЛЏЪБЪЧжБЯпACЙ§ЕуOЃЌгЩДЫЕУЕНHAЃНmЃН![]() ЃЌдйЧѓГіBHЃЌИљОнЩфгАЖЈРэЧѓГіOAЃЌдйЧѓГіOBЃЌЕУЕНЕуAЁЂBЕФзјБъМДПЩЧѓГіжБЯпABЕФНтЮіЪНЃЛ
ЃЌдйЧѓГіBHЃЌИљОнЩфгАЖЈРэЧѓГіOAЃЌдйЧѓГіOBЃЌЕУЕНЕуAЁЂBЕФзјБъМДПЩЧѓГіжБЯпABЕФНтЮіЪНЃЛ
ЃЈ3ЃЉЗжСНжжЧщПіЃКЂйЕБ0ЁмmЁм![]() ЪБЃЌЂкЕБ
ЪБЃЌЂкЕБ![]() ЃМmЁм
ЃМmЁм![]() ЪБЃЌЧѓSЙигкmЕФНтЮіЪН
ЪБЃЌЧѓSЙигкmЕФНтЮіЪН
ЃЈ1ЃЉДгЭМ2ПЩЕУЃКABЃН2![]() ЃЌ
ЃЌ
mЃН0ЪБЃЌЭМЯѓУЛгаЦНвЦЃЌдђДЫЪБaЃНSЁїABCЃН![]() AB2ЃН10ЃЌ
AB2ЃН10ЃЌ
ЙЪД№АИЮЊЃК10ЃЛ
ЃЈ2ЃЉЙ§ЕуOзї![]() ЃЌ
ЃЌ
ЕББпACЙ§ЕуOЪБЃЌSЕФБэДяЪНЗЂЩњБфЛЏЃЌДЫЪББпACвЦЖЏЕНHCЁфЫљДІЕФЮЛжУЃЌ

дђHAЃНmЃН![]() ЃЌBHЃНABЉAHЃН
ЃЌBHЃНABЉAHЃН![]() ЃЌ
ЃЌ
ЖјOH2ЃНHAHBЃН![]() ЃЌдђOAЃН2ЃЌ
ЃЌдђOAЃН2ЃЌ
ЖјAB2ЃН20ЃЌЙЪOBЃН4ЃЌдђЕуAЁЂBЕФзјБъЗжБ№ЮЊЃКЃЈ2ЃЌ0ЃЉЁЂЃЈ0ЃЌ4ЃЉЃЌ
НЋЕуAЁЂBЕФзјБъДњШывЛДЮКЏЪ§БэДяЪНВЂНтЕУЃК
жБЯпABЕФБэДяЪНЮЊЃКyЃНЉ![]() x+4ЃЛ
x+4ЃЛ
ЃЈ3ЃЉЂйЕБ0ЁмmЁм![]() ЪБЃЌ
ЪБЃЌ
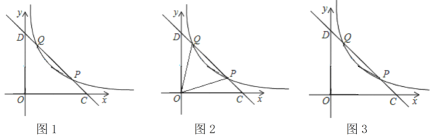
ШчЭМ1зѓЭМЫљЪОЃЌЩшБпAЁфCЁфНЛxжсгкЕуHЃЌ
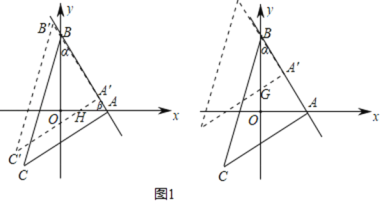
дђAЁфHЃНAAЁфtanІТЃЌ
SЃНSЫФБпаЮBAЁфHOЃНSЁїABOЉSЁїAAЁфHЃН![]() OAЁСOBЉ
OAЁСOBЉ![]() AЁфAЁСAЁфHЃН
AЁфAЁСAЁфHЃН![]()
![]() ЁСm2ЁС
ЁСm2ЁС![]() ЃН
ЃН![]() Љ
Љ![]() m2ЃЌ
m2ЃЌ
ЕБmЃН![]() ЪБЃЌSЃН
ЪБЃЌSЃН![]() ЃНbЃЌ
ЃНbЃЌ
ЂкЕБ![]() ЃМmЁм
ЃМmЁм![]() ЪБЃЌ
ЪБЃЌ
ШчЭМ1гвЭМЫљЪОЃЌЩшБпAЁфCЁфНЛyжсгкЕуGЃЌ
SЃНSЁїAЁфBGЃН![]() ЁСAЁфBЁСAЁфGЃН
ЁСAЁфBЁСAЁфGЃН![]() ЁСABЁф2ЁСtanІСЃН
ЁСABЁф2ЁСtanІСЃН![]() ЁСЃЈ
ЁСЃЈ![]() ЉmЃЉ2ЃН
ЉmЃЉ2ЃН![]() ЃЈ
ЃЈ![]() ЉmЃЉ2ЃЛ
ЉmЃЉ2ЃЛ
злЩЯЃЌSЃН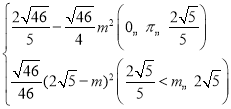 .
.

 ПЊаФЪдОэЦкФЉГхДЬ100ЗжЯЕСаД№АИ
ПЊаФЪдОэЦкФЉГхДЬ100ЗжЯЕСаД№АИ ЫЋЛљЭЌВНЕМКНбЕСЗЯЕСаД№АИ
ЫЋЛљЭЌВНЕМКНбЕСЗЯЕСаД№АИ ЛЦИдаЁзДдЊЭЌВНМЦЫуЬьЬьСЗЯЕСаД№АИ
ЛЦИдаЁзДдЊЭЌВНМЦЫуЬьЬьСЗЯЕСаД№АИ