题目内容
【题目】在平面直角坐标系中，A
，B
，C
，点P为任意一点，已知PA⊥PB，则线段PC的最大值为（ ）
A.3B.5C.8D.10
【答案】C
【解析】
连接OC、OP、PC由PA⊥PB可得点P在以O为圆心，AB长为直径的圆上；再根据三角形的三边关系可得CP≤OP+OC，则当当点P，O，C在同一直线上， CP的最大值为OP+OC的长，然后进行计算即可.
解：如图所示，连接OC、OP、PC
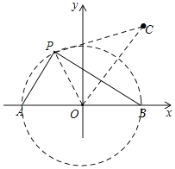
∵PA⊥PB，
∴点P在以O为圆心，AB长为直径的圆上，
∵△COP
∴CP≤OP+OC，
∴当点P，O，C在同一直线上，且点P在CO延长线上时，CP的最大值为OP+OC的长，
又∵A（-3，0），B（3，0），C（3，4），
∴AB=6，OC=5，OP=
AB=3，
∴线段PC的最大值为OP+OC=3+5=8，
故答案为C．
练习册系列答案
相关题目
