题目内容
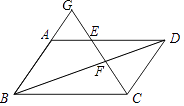
【题目】如图,在梯形ABCD中,AD∥BC,AC与BD相交于点O,AC=BC,点E在DC的延长线上,∠BEC=∠ACB,已知BC=9,cos∠ABC= ![]() .
.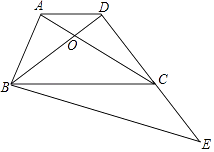
(1)求证:BC2=CDBE;
(2)设AD=x,CE=y,求y与x之间的函数解析式,并写出定义域;
(3)如果△DBC∽△DEB,求CE的长.
【答案】
(1)
解:∵∠DCB=∠ACD+∠ACB,∠DCB=∠EBC+∠BEC,∠ACB=∠BEC,
∴∠ACD=∠EBC,
∵AD∥BC,
∴∠DAC=∠ACB=∠CEB,
∴△DAC∽△CEB,
∴ ![]() =
= ![]() ,
,
∴BCAC=CDBE,
∵AC=BC,
∴BC2=CDBF.
(2)
解:过点C作CF⊥AB于F,AG⊥BC于G,DH⊥BC于H.
在Rt△CBF中,BF=BCcos∠ABC=9× ![]() =3,
=3,
∴AB=6,
在Rt△ABG中,BG=ABcos∠ABC=6× ![]() =2,
=2,
∵AD∥BC,DH=AG,
∴DH2=AG2=AB2﹣BG2=62﹣22=32,
∵AG∥DH,
∴GH=AD=x,
∴CH=BC﹣BG﹣GH=7﹣x,
∴CD= ![]() =
= ![]() =
= ![]() ,
,
∵△CEB∽△DAC,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴y= ![]() ,
,
∴y= ![]() (x>0且x≠9)
(x>0且x≠9)
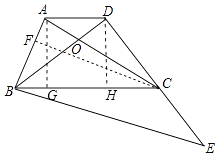
(3)
解:∵△DBC∽△DEB,∠CDB=∠BDE,∠CBD<∠DBC,
∴∠DBC=∠DEB=∠ACB,
∴OB=OC,
∵AD∥BC,
∴ ![]() =
= ![]() ,
,
∴AC=BD,
∴四边形ABCD是等腰梯形,
∴AB=CD,∠ABC=∠DCB,
∵∠AGB=∠DHC=90°,
∴△ABG≌△DCH,
∴CH=BG=2,
∴x=GH=BC﹣BG﹣CH=9﹣2﹣2=5.
∴CE=y= ![]()
【解析】(1)只要证明△DAC∽△CEB,得到 ![]() =
= ![]() ,再根据题意AC=BC,即可证明.(2)过点C作CF⊥AB于F,AG⊥BC于G,DH⊥BC于H.由△CEB∽△DAC,得
,再根据题意AC=BC,即可证明.(2)过点C作CF⊥AB于F,AG⊥BC于G,DH⊥BC于H.由△CEB∽△DAC,得 ![]() =
= ![]() ,由此即可解决问题.(3)首先证明四边形ABCD是等腰梯形,再证明△ABG≌△DCH,推出CH=BG=2,推出x=GH=BC﹣BG﹣CH=9﹣2﹣2=5,再利用(2)中即可即可解决问题.
,由此即可解决问题.(3)首先证明四边形ABCD是等腰梯形,再证明△ABG≌△DCH,推出CH=BG=2,推出x=GH=BC﹣BG﹣CH=9﹣2﹣2=5,再利用(2)中即可即可解决问题.
【考点精析】认真审题,首先需要了解梯形的定义(一组对边平行,另一组对边不平行的四边形是梯形.两腰相等的梯形是等腰梯形),还要掌握直角梯形(一腰垂直于底的梯形是直角梯形)的相关知识才是答题的关键.

 阅读快车系列答案
阅读快车系列答案