题目内容
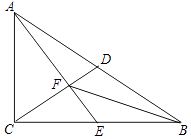
【题目】如图,在平行四边形ABCD中,点E在边AD上,联结CE并延长,交对角线BD于点F,交BA的延长线于点G,如果DE=2AE,那么CF:EF:EG= . 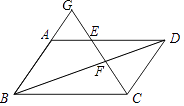
【答案】6:4:5
【解析】解:设AE=x,则DE=2x, ∵四边形ABCD是平行四边形,
∴BC=AD=AE+DE=3x,AD∥BC,
∴△GAE∽△GBC,△DEF∽△BCF,
∴ ![]() =
= ![]() =
= ![]() ,
, ![]() =
= ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
设EF=2y,则CF=3y,
∴EC=EF+CF=5y,
∴GE= ![]() y,
y,
则CF:EF:EG=3y:2y: ![]() y=6:4:5,
y=6:4:5,
故答案为:6:4:5.
设AE=x,则DE=2x,由四边形ABCD是平行四边形得BC=AD=AE+DE=3x,AD∥BC,证△GAE∽△GBC、△DEF∽△BCF得 ![]() =
= ![]() =
= ![]() 、
、 ![]() =
= ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,设EF=2y,则CF=3y、GE=
,设EF=2y,则CF=3y、GE= ![]() y,从而得出答案.
y,从而得出答案.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案
相关题目