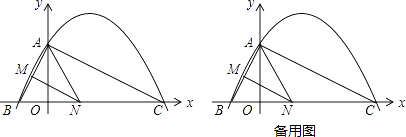题目内容
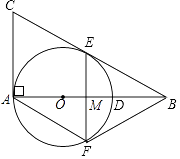
【题目】综合探究：如图1，在平面直角坐标系xOy中，抛物线y=﹣ 
与x轴交于点A（﹣6，0）和点B（点A在点B左侧），与y轴交于点C，点P为线段AO上的一个动点，过点P作x轴的垂线l与抛物线交于点E，连接AE，EC．
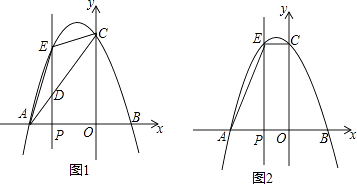
（1）求抛物线的表达式及点C的坐标；
（2）连接AC交直线l于点D，则在点P运动过程中，当点D为EP中点时，S△ADP：S△CDE=；
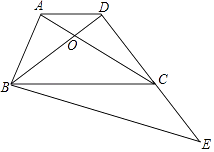
（3）如图2，当EC∥x轴时，点P停止运动，此时，在抛物线上是否存在点G，使得以点A，E，G为顶点的三角形是直角三角形？若存在，请求出点G的坐标，若不存在，说明理由．
【答案】
（1）
解：∵点A（﹣6，0）在抛物线y=﹣ 
x2+bx+8上，
∴0=﹣ （﹣6）2+b（﹣6）+8，
∴b=﹣ 
，
∴y=﹣ x2﹣ x+8，
令x=0，y=8，
∴C（0，8）
（2）1：2
（3）
解：存在点G使得以点A，E，G为顶点的三角形为直角三角形，
连接EG，AG，作GM⊥l，GN⊥x轴，
∵EC∥x轴，
∴EP=CO=8，
把y=8代入y=﹣ x2﹣ x+8，
∴8=﹣ x2﹣ x+8，
∴x=0（舍），或x=﹣2，
∴P（﹣2，0），
∴AP=AO﹣PO=4，
Ⅰ、如图1，
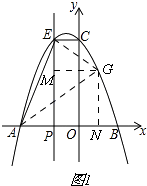
当∠AEG=90°时，
∴∠MEG+∠AEP=90°，
∵∠AEP+∠EAP=90°，
∴∠MEG=∠EAP，
∵∠APE=∠EMG=90°，
∴△EMG∽△APE，
∴ 
，
设点G（m，﹣ m2﹣ m+8）（m＞0），
∴GN=MP=﹣ m2﹣ m+8，
∴EM=EP﹣MP=8﹣（﹣ m2﹣ m+8）=y= m2+ m，
MG=PN=PO+ON=2+m，
∵ ，
∴ 
，
∴m=﹣2（舍）或m= 
，
∴G（ ， 
）；
Ⅱ、如图2，
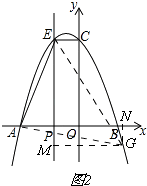
当∠EAG=90°时，
∴∠NAG+∠EAP=90°，
∵∠AEP+∠EAP=90°，
∴∠NAG=∠AEP，
∵∠APE=∠GNA=90°，
∴△GNA∽△APE，
∴ 
，
设点G（n，﹣ n2﹣ n+8）（n＞0，﹣ n2﹣ n+8＜0），
∴GN= m2+ m+8，
∴AN=AO+ON=6+n，
∵ ，
∴ 
，
∴n=﹣6（舍），或n= 
，
∴G（ ，﹣ 
），
符合条件的G点的坐标为G（ ， ）或G（ ，﹣ ）
【解析】解：（2）设E（m，﹣ m2﹣ m+8），
∴P（m，0），
∵点D为EP中点，
∴DP=DE，D（m，﹣ 
m2+﹣ x+4），
∵A（﹣6，0），C（0，8），
∴直线AC解析式为y= 
x+8，
∵点D在直线AC上，
∴ m+8=﹣ m2+﹣ x+4，
∴m=﹣6（舍）或m=﹣4，
∴P（﹣4，0）
∴AP=2，OP=4，
∴ 
；
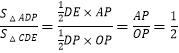所以答案是1：2（1）用待定系数法求出抛物线解析式，令x=0求出y轴交点坐标；（2）先确定出直线AC解析式为y= x+8，设出点E的坐标，表示出点D（m，﹣ m2+﹣ x+4），而点D在直线AC上，列出方程 m+8=﹣ m2+﹣ x+4，求出m，从而得出结论；（3）先求出点P的坐标，再分两种情况计算Ⅰ、当∠AEG=90°时，判断出△EMG∽△APE，得出比例式求解即可，Ⅱ、当∠EAG=90°时，判断出△GNA∽△APE，得到比例式计算．
【考点精析】掌握二次函数的概念和二次函数的图象是解答本题的根本，需要知道一般地，自变量x和因变量y之间存在如下关系：一般式：y=ax2+bx+c(a≠0，a、b、c为常数)，则称y为x的二次函数；二次函数图像关键点：1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点．
