题目内容
 是等边三角形,点
是等边三角形,点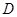 是射线
是射线 上的一个动点(点
上的一个动点(点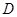 不与点
不与点 重合),
重合), 是以
是以 为边的等边三角形,过点
为边的等边三角形,过点 作
作 的平行线,分别交射线
的平行线,分别交射线 于点
于点 ,连接
,连接 .
.
(1)如图(a)所示,当点
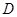 在线段
在线段 上时,
上时,①求证:
 ;
;②探究:四边形
 是怎样特殊的四边形?并说明理由;
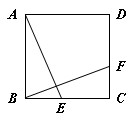
是怎样特殊的四边形?并说明理由;(2)如图(b)所示,当点
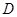 在
在 的延长线上时,
的延长线上时,①第(1)题中所求证和探究的两个结论是否仍然成立?(直接写出,不必说明理由)
②当点
 运动到什么位置时,四边形
运动到什么位置时,四边形 是菱形?并说明理由.
是菱形?并说明理由.(1)①见解析,②平行四边形(2)①成立,②BC=CD
解:(1) ① ∵ △ABC和△ADE都是等边三角形,
∴ AE=AD,AB=AC,∠EAD=∠BAC=60°.
又∵ ∠EAB=∠EAD-∠BAD,∠DAC=∠BAC-∠BAD
∴ ∠EAB=∠DAC,
∴ △AEB≌△ADC. ………………………………………………………(3分)
② 四边形 是平行四边形. ………………………………………(6分)
是平行四边形. ………………………………………(6分)
(2)(1)中的结论:
① △AEB≌△ADC,② 四边形 是平行四边形,均成立. ……………………(8分)
是平行四边形,均成立. ……………………(8分)
(3)当BC=CD时,四边形BCFE是菱形.……………………………………………(9分)
理由: 由①得△AEB≌△ADC,
∴BE=BC
又∵ BE=CD,
∴ BC=CD.
由②得四边形 是平行四边形,
是平行四边形,
∴ 四边形 是菱形. ……………………………………………(13分)
是菱形. ……………………………………………(13分)
(1)①证明:因∠EAB+∠BAD=∠BAD+∠DAC=60度,所以∠EAB=∠DAC,又EA=DA,BA=CA,故△AEB≌△ADC.。②于是∠EBC=∠EBA+∠ABC=∠DCA+∠ABC=120度。那么∠EBC+∠BCG=120度+60度=180度,于是EB//GC,又EG//BC,故BCGE为一平行四边形。 (2)BEGC仍为平行四边形。与(1)类似,容易证明:ΔABE全等于ΔACD,那么∠ABE=∠ACD=120度,于是∠CBE=∠ACB=60度,进而BE//GC,又BC//EG,从而得证。(3)欲使其成为菱形,只须BE=BC,又BE=CD,故只须选取D点使BC=CD即可。
∴ AE=AD,AB=AC,∠EAD=∠BAC=60°.
又∵ ∠EAB=∠EAD-∠BAD,∠DAC=∠BAC-∠BAD
∴ ∠EAB=∠DAC,
∴ △AEB≌△ADC. ………………………………………………………(3分)
② 四边形
 是平行四边形. ………………………………………(6分)
是平行四边形. ………………………………………(6分)(2)(1)中的结论:
① △AEB≌△ADC,② 四边形
 是平行四边形,均成立. ……………………(8分)
是平行四边形,均成立. ……………………(8分)(3)当BC=CD时,四边形BCFE是菱形.……………………………………………(9分)
理由: 由①得△AEB≌△ADC,
∴BE=BC
又∵ BE=CD,
∴ BC=CD.
由②得四边形
 是平行四边形,
是平行四边形,∴ 四边形
 是菱形. ……………………………………………(13分)
是菱形. ……………………………………………(13分)(1)①证明:因∠EAB+∠BAD=∠BAD+∠DAC=60度,所以∠EAB=∠DAC,又EA=DA,BA=CA,故△AEB≌△ADC.。②于是∠EBC=∠EBA+∠ABC=∠DCA+∠ABC=120度。那么∠EBC+∠BCG=120度+60度=180度,于是EB//GC,又EG//BC,故BCGE为一平行四边形。 (2)BEGC仍为平行四边形。与(1)类似,容易证明:ΔABE全等于ΔACD,那么∠ABE=∠ACD=120度,于是∠CBE=∠ACB=60度,进而BE//GC,又BC//EG,从而得证。(3)欲使其成为菱形,只须BE=BC,又BE=CD,故只须选取D点使BC=CD即可。

练习册系列答案
相关题目
 ,点E是AD边的中点,点M是AB边上一动点(不与点A重合),延长ME交射线CD于点N,连接MD,AN.
,点E是AD边的中点,点M是AB边上一动点(不与点A重合),延长ME交射线CD于点N,连接MD,AN.

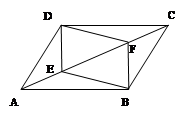
 中,
中,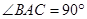 ,延长
,延长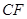 到
到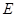 ,使
,使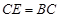 ,过
,过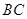 的垂线,交
的垂线,交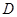 .
. 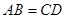 .
.
