题目内容
如图，在菱形ABCD中，AB=2，
,点E是AD边的中点，点M是AB边上一动点（不与点A重合），延长ME交射线CD于点N，连接MD，AN.
（1）求证：四边形AMDN是平行四边形；
（2）填空：①当AM的值为 时，四边形AMDN是矩形；
②当AM的值为 时，四边形AMDN是菱形。
,点E是AD边的中点，点M是AB边上一动点（不与点A重合），延长ME交射线CD于点N，连接MD，AN.（1）求证：四边形AMDN是平行四边形；
（2）填空：①当AM的值为 时，四边形AMDN是矩形；
②当AM的值为 时，四边形AMDN是菱形。
（1）见解析（2）①1；②2
（1）证明：∵四边形ABCD是菱形，∴ND∥AM
∴
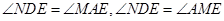
又∵点E是AD中点，∴DE=AE
∴
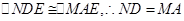
∴四边形AMDN是平行四边形
（2）①当AMDN为矩形时，AD=MN=2，E为MN和AD中点
∴ME=ME=1
∵，∴△AME是等边三角形，∴AM=1
②当四边形AMDN是菱形时，MN⊥AD
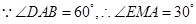
∴AM=2AE=2
∴
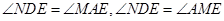
又∵点E是AD中点，∴DE=AE
∴
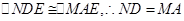
∴四边形AMDN是平行四边形
（2）①当AMDN为矩形时，AD=MN=2，E为MN和AD中点
∴ME=ME=1
∵
，∴△AME是等边三角形，∴AM=1②当四边形AMDN是菱形时，MN⊥AD
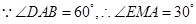
∴AM=2AE=2
练习册系列答案
相关题目
是等边三角形，点
是射线
上的一个动点（点
重合），
是以
为边的等边三角形，过点
作
于点
，连接
．
；
是怎样特殊的四边形？并说明理由；
沿直线
折叠，顶点
恰好落在
边上
点处，已知
，
，则图中阴影部分面积为 __.
=4,O为对角线BD的中点，过O点作OE⊥AB，垂足为E．
的长．
.
；