题目内容
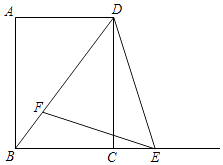
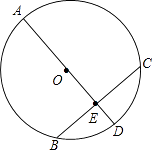
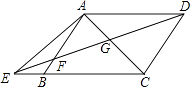
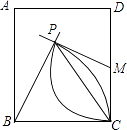
【题目】将笔记本电脑放置在水平桌面上,显示屏OB与底板OA夹角为115°(如图1),侧面示意图为图2;使用时为了散热,在底板下面垫入散热架O′AC后,电脑转到AO′B′的位置(如图3),侧面示意图为图4,已知OA=0B=20cm,B′O′⊥OA,垂足为C. 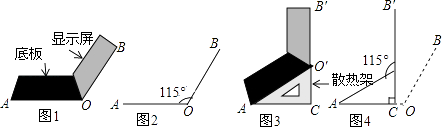
(1)求点O′的高度O′C;(精确到0.1cm)
(2)显示屏的顶部B′比原来升高了多少?(精确到0.1cm)
(3)如图4,要使显示屏O′B′与原来的位置OB平行,显示屏O′B′应绕点O′按顺时针方向旋转多少度? 参考数据:(sin65°=0.906,cos65°=0.423,tan65°=2.146.cot65°=0.446)
【答案】
(1)解:∵B′O′⊥OA,垂足为C,∠AO′B=115°,
∴∠AO′C=65°,
∵cos∠CO′A= ![]() ,
,
∴O′C=O′Acos∠CO′A=20cos65°=8.46≈8.5(cm)
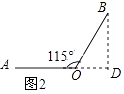
(2)解:如图2,过B作BD⊥AO交AO的延长线于D,
∵∠AOB=115°,
∴∠BOD=65°,
∵sin∠BOD= ![]() ,
,
∴BD=OBsin∠BOD=20×sin65°=18.12,
∴O′B′+O′C﹣BD=20+8.46﹣18.12=10.34≈10.3(cm),
∴显示屏的顶部B′比原来升高了10.3cm
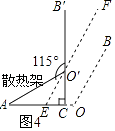
(3)解:如图4,过O′作EF∥OB交AC于E,
∴∠FEA=∠BOA=115°,
∠FOB′=∠EO′C=∠FEA﹣∠O′CA=115°﹣90°=25°,
∴显示屏O′B′应绕点O′按顺时针方向旋转25度
【解析】(1)解直角三角形即可得到结论;(2)如图2,过B作BD⊥AO交AO的延长线于D,根据三角函数的定义即可得到结论;(3)如图4,过O′作EF∥OB交AC于E,根据平行线的性质得到∠FEA=∠BOA=115°,于是得到结论.