��Ŀ����
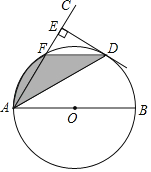
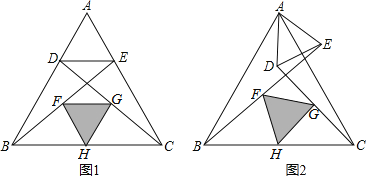
����Ŀ����ͼ1���ڵȱߡ�ABC�У���D��E�ֱ��ڱ�AB��AC�ϣ�AD��AE������BE��CD����F��G��H�ֱ���BE��CD��BC���е�
(1)�۲���룺ͼ1�У���FGH����״��______.
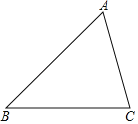
(2)̽��֤�����ѡ�ADE�Ƶ�A��ʱ�뷽����ת��ͼ2��λ�ã���FGH����״�Ƿ����ı䣿��˵�����ɣ�
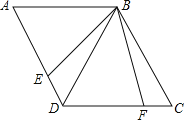
(3)��չ���죺�ѡ�ADE�Ƶ�A��ƽ����������ת����AD��2��AB��6����ֱ��д����FGH���ܳ������ֵ.
���𰸡�(1)�ȱ������Σ�(2)�������ı䣬���ɼ�������(3)��PMN���ܳ������ֵΪ12.
��������
(1)�۲���룺
��ͼ1���ȸ��ݵȱ������ε����ʵõ�AB��AC����ABC����ACB��60������BD��CE���ٸ�����������λ�����ʵ�FH��CE��FH��![]() CE��GH��AD��GH��
CE��GH��AD��GH��![]() BD���Ӷ��õ�FH��GH����FHG��60�����Ӷ����ж���FGHΪ�ȱ������Σ�
BD���Ӷ��õ�FH��GH����FHG��60�����Ӷ����ж���FGHΪ�ȱ������Σ�
(2)̽��֤����
����CE��BD����ͼ2����������ת�Ķ��壬����ABD�Ƶ�A��ʱ����ת60���ɵõ���CAE����BD��CE����ABD����ACE����(1)һ���ɵ�FH��CE��FH��![]() CE��GH��AD��GH��
CE��GH��AD��GH��![]() BD���ɵ�FH��GH����BHF����BCE����CHG����CBD����������BHF+��CHG��120�����Ӷ��õ���FHG��60�������ǿ��ж���FHGΪ�ȱ�������.
BD���ɵ�FH��GH����BHF����BCE����CHG����CBD����������BHF+��CHG��120�����Ӷ��õ���FHG��60�������ǿ��ж���FHGΪ�ȱ�������.
(3)��չ���죺
����AB��AD��BD��AB+AD(���ҽ�����B��A��D����ʱȡ�Ⱥ�)�õ�BD�����ֵΪ8����GH�����ֵΪ4��Ȼ���ȷ����FHG���ܳ������ֵ.
�⣺(1)�۲���룺
��ͼ1���ߡ�ABCΪ�ȱ������Σ�
��AB��AC����ABC����ACB��60����
��AD��AE��
��BD��CE��
�ߵ�F��G��H�ֱ���BE��CD��BC���е�
��FH��CE��FH��![]() CE��GH��AD��GH��
CE��GH��AD��GH��![]() BD��
BD��
��FH��GH����BHF����BCA��60������CHG����CBA��60����
���FHG��60����
���FGHΪ�ȱ������Σ�
�ʴ�Ϊ���ȱ������Σ�
(2)̽��֤����
��PMN����״�������ı䣬��ȻΪ�ȱ�������.
�������£�����CE��BD����ͼ2��
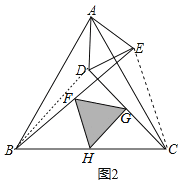
��AB��AC��AE��AD����BAC����DAE��60����
�����ABD�Ƶ�A��ʱ����ת60���ɵõ���CAE��
���ABD�ա�ACE��
��BD��CE����ABD����ACE��
��(1)һ���ɵ�FH��CE��FH��![]() CE��GH��AD��GH��
CE��GH��AD��GH��![]() BD��
BD��
��FH��GH����BHF����BCE����CHG����CBD��
���BHF+��CHG����BCE+��CBD����ABC����ABD+��ACB+��ACE��60��+60����120����
���FHG��60����
���FHGΪ�ȱ�������.
(3)��չ���죺
��GH��![]() BD��
BD��
�൱BD��ֵ���ʱ��GH��ֵ���
��AB��AD��BD��AB+AD(���ҽ�����B��A��D����ʱȡ�Ⱥ�)
��BD�����ֵΪ2+6��8��
��GH�����ֵΪ4��
���PMN���ܳ������ֵΪ12.

����Ŀ��ij��������һ����Ʒ���ɱ�ÿǧ��40Ԫ���涨ÿǧ���ۼ۲����ڳɱ����Ҳ�����80Ԫ�����г����飬ÿ���������y��ǧ�ˣ���ÿǧ���ۼ�x��Ԫ������һ�κ�����ϵ�������������±���
�ۼ�x��Ԫ/ǧ�ˣ� | 50 | 60 | 70 |
������y��ǧ�ˣ� | 100 | 80 | 60 |
��1����y��x֮��ĺ�������ʽ��
��2������Ʒÿ���������ΪW��Ԫ�������ۼ�x��Ϊ����Ԫʱ������ÿ���ܻ�����������������Ƕ��٣�
��3���������Ҫ���ÿ�첻����1350Ԫ�������ҷ��ϳ����Լ��Ĺ涨����ô����Ʒÿǧ���ۼ۵�ȡֵ��Χ�Ƕ��٣���˵�����ɣ�