题目内容
【题目】（问题背景）先阅读理解下面的例题，再按要求解答下列问题：
例题：解一元二次不等式x2﹣4＞0
（问题解决）∵x2﹣4＝（x+2）（x﹣2）
∴x2﹣4＞0可化为（x+2）（x﹣2）＞0
由有理数的乘法法则“两数相乘，同号得正”，得
解不等式组①，得x＞2，
解不等式组②，得x＜﹣2，
∴（x+2）（x﹣2）＞0的解集为x＞2或x＜﹣2，
即一元二次不等式 x2﹣4＞0 的解集为x＞2或x＜﹣2．
（问题应用）（1）一元二次不等式 x2﹣16＞0 的解集为 ；
（2）分式不等式
＞0 的解集为 ；
（3）（拓展应用）解一元二次不等式 2x2﹣3x＜0．
【答案】（1）x＞4或x＜﹣4；（2）x＞3或x＜1；（3）0＜x＜
【解析】
（1）将一元二次不等式的左边因式分解后化为两个一元一次不等式组求解即可；
（2）据分式不等式大于零可以得到其分子、分母同号，从而转化为两个一元一次不等式组求解即可；
（3）将一元二次不等式的左边因式分解后化为两个一元一次不等式组求解即可．
解：问题应用：（1）∵x2-16=（x+4）（x-4）
∴x2-16＞0可化为
（x+4）（x-4）＞0
由有理数的乘法法则“两数相乘，同号得正”，得
①
②
解不等式组①，得x＞4，
解不等式组②，得x＜-4，
∴（x+4）（x-4）＞0的解集为x＞4或x＜-4，
即一元二次不等式x2-16＞0的解集为x＞4或x＜-4；
（2）
＞0
∴
或
解得：x＞3或x＜1 ；
（3）拓展应用：∵2x2﹣3x＝x（2x﹣3）
∴2x2﹣3x＜0可化为
x（2x﹣3）＜0
∴
① 或
②
解不等式组①，得0＜x＜，
解不等式组②，无解 ，
∴不等式2x2﹣3x＜0的解集为0＜x＜．
【题目】为了解今年我校初三学生中考体育测试成绩，现对今年我校初三中考体育测试成绩进行抽样调查，结果统计如下，其中扇形统计图中C组所在的扇形的圆心角为36°，组别成绩（分）频数．
组别 | 成绩（分） | 频数 |
A | 30＜x≤34 | 1 |
B | 34＜x≤38 | 1 |
C | 38＜x≤42 | 6 |
D | 42＜x≤46 | b |
E | 46＜x≤50 | 30 |
合计 | a | |
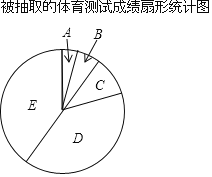
根据上面图标提供的信息，回答下列问题：
（1）计算频数分布表中a与b的值；
（2）根据C组38＜x≤42的组中间值40，估计C组中所有数据的和为 ；
（3）请估计今年我校初三学生中考体育成绩的平均分（结果取整数）．
