题目内容
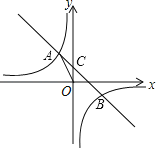
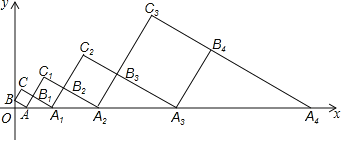
【题目】如图所示，在平面直角坐标系中，点A（
，0）、B（0，
），以AB为边作正方形ABCB1，延长CB1交x轴于点A1，以A1B1为边作正方形A1B1C1B2，延长C1B2交x轴于点A2，以A2B2为边作正方形A2B2C2B3，延长C2B3交x轴于点A3，以A3B3为边作正方形A3B3C3B4，…，依此规律，则△A6B7A7的周长为_____．
【答案】
【解析】
利用相似三角形的性质，探究规律，利用规律解决问题即可．
解：由题意：A1B1∥A2B2，
∴∠AA1B1＝∠A1A2B2，
∵∠AB1A1＝∠A1B2A2＝90°，
∴△AB1C1∽△A1B2C2，
∴
，
∵△AB1A1的周长为3+
，△A1B2A2的周长为（3+），△A2B3A3的周长为（3+）（）2，…，△AnBn+1An+1的周长为（3+）（）n，
∴△A6B7A7的周长为（3+）（）6＝27（3+）．
故答案为：27（3+）．
练习册系列答案
相关题目
