Question

【题目】在Rt△ABC中，∠C＝90°，AB＝10cm，AC＝8cm，点P为边AC上一点，且AP＝5cm．点Q为边AB上的任意一点（不与点A，B重合），若点A关于直线PQ的对称点A'恰好落在△ABC的边上，则AQ的长为_____cm．

Answer 1

【答案】或4．

【解析】

由对称可知AP=A'P，AQ=A'Q，由勾股定理可计算A'C，A'P，作A'H⊥AB构造直角三角形，用勾股定理列方程组即可计算AQ的长．

在Rt△ABC中，∠C＝90°，AB＝10cm，AC＝8cm，

∴BC＝6cm，

①若点A'落在BC上，如图：

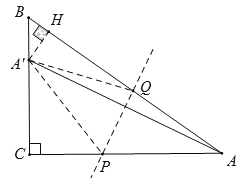
点A关于直线PQ的对称点A'，

∵点A关于直线PQ的对称点A'，

∴A'Q＝AQ，AP＝A'P，

∵AP＝5，

∴PC＝3，A'C＝4，A'B＝2，

∴A'A＝4，

作A'H垂直AB，由勾股定理可得：

，

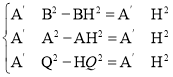设AQ＝AQ'＝x，BH＝y，

∴，

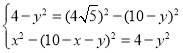解得：，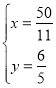

故AQ的长为．

②若点A'落在AB上，如图：

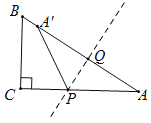
∵点A关于直线PQ的对称点A'，

∴PQ⊥AB，

∴△APQ～△ABC，

∴，

∴，

∴AQ＝4．

综上所述：若点A关于直线PQ的对称点A'恰好落在△ABC的边上，则AQ的长为或4cm．

故答案为或4．