题目内容
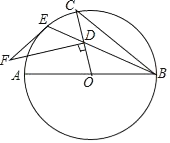
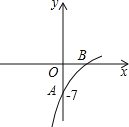
【题目】已知抛物线y=(1-a)x2+8x+b的图象的一部分如图所示,抛物线的顶点在第一象限,且经过点A(0,-7)和点B.
(1)求a的取值范围;
(2)若OA=2OB,求抛物线的解析式.
【答案】(1)a的取值范围是1<a<![]() ;(2)y=-
;(2)y=-![]() x2+8x-7.
x2+8x-7.
【解析】
(1)因为二次函数过点A,所以可以确定b的值,又因为抛物线为y=(1-a)x2+8x-7又抛物线的顶点在第一象限,开口向下,所以抛物线与x轴有两个不同的交点,所以可以确定1-a<0,△>0,解不等式组即可求得a的取值范围;
(2)因为OA=2OB,可求得点B的坐标,将点A,B的坐标代入二次函数的解析式即可求得a,b的值,即可求得二次函数的解析式.
(1)由图可知,b=-7.
故抛物线为y=(1-a)x2+8x-7.
又因抛物线的顶点在第一象限,开口向下,
所以抛物线与x轴有两个不同的交点.
∴ ,
,
解之,得1<a<![]() .
.
即a的取值范围是1<a<![]() .
.
(2)设B(x1,0),
由OA=20B,
得7=2x1,即x1=![]() .
.
由于x1=![]() ,方程(1-a)x2+8x-7=0的一个根,
,方程(1-a)x2+8x-7=0的一个根,
∴(1-a)(![]() )2+8×
)2+8×![]() -7=0
-7=0
∴![]() .
.
故所求所抛物线解析式为y=-![]() x2+8x-7.
x2+8x-7.

【题目】某水果批发市场香蕉的价格如下表
购买香蕉数(千克) | 不超过20千克 | 20千克以上但不超过40千克 | 40千克以上 |
每千克的价格 | 6元 | 5元 | 4元 |
张强两次共购买香蕉50千克,已知第二次购买的数量多于第一次购买的数量,共付出264元,请问张强第一次,第二次分别购买香蕉多少千克?
【题目】北京市环境保护监测中心每月向公众公布北京市各区域的空气质量状况.2019年1月份各区域的![]() 浓度情况如表:
浓度情况如表:
各区域1月份![]() 浓度(单位:微粒/立方米)表
浓度(单位:微粒/立方米)表
区域 |
| 区域 |
| 区域 |
|
怀柔 | 33 | 海淀 | 50 | 平谷 | 45 |
密云 | 34 | 延庆 | 51 | 丰台 | 61 |
门头沟 | 41 | 西城 | 61 | 大兴 | 72 |
顺义 | 41 | 东城 | 60 | 开发区 | 65 |
昌平 | 38 | 石景山 | 55 | 房山 | 62 |
朝阳 | 54 | 通州 | 57 |
从上述表格随机选择一个区域,其2019年1月份![]() 的浓度小于51微克/立方米的概率是______.
的浓度小于51微克/立方米的概率是______.