题目内容
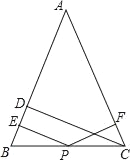
【题目】已知：如图，△ABC，△ADE均为等腰直角三角形，点D，E，C在同一直线上，连接BD．
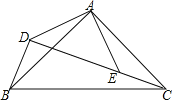
（1）求证：△ADB≌△AEC；
（2）若AD=AE=
，CE=2，求BC的长．
【答案】（1）详见解析；（2）
.
【解析】
(1)由题意可得AD=AE，AB=AC，∠DAB=∠EAC，可得证明；
（2）可得DE=2，BD=CE=2，可得∠AEC=135°，∠ADB=135°，∠BDC=90°，可得BC的值.
证明：（1）∵△ABC和△ADE都是等腰直角三角形，
∴AD=AE，AB=AC，∠DAE=∠BAC，
∴∠DAB=∠EAC，
在△ADB和△AEC中，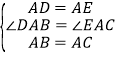
，
∴△ADB≌△AEC（SAS），
（2）∵△ADB≌△AEC
∴BD=CE，∠AEC=∠ADB，
∴DE=2，BD=CE=2，
∵∠AEC=135°，
∴∠ADB=135°，
∴∠BDC=90°，
∴BC=
练习册系列答案
相关题目
