题目内容
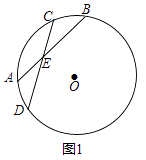
【题目】已知，⊙O的两条弦AB、CD相交于点E，
（1）如图1，若BE=DE，求证： 
= 
； 
（2）如图2，在（1）的条件下，连接OC，AP为⊙O的直径，PQ为⊙O的弦，且PQ∥AB，求证：∠OCD=∠APQ； 
（3）如图3，在（2）的条件下，连接BD分别与OA、OC交于点G、H，连接DQ，设CD与AP交于点F， 若PQ=2CF，BH=5GH，DQ=4，求⊙O的半径．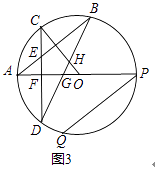
【答案】
（1）证明：连接AD、BC，
∵ 
= ，
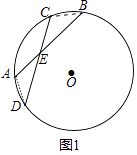
∴∠B=∠D，
在△AED和△CEB中，
，
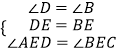∴△AED≌△CEB，
∴AD=BC，
∴ 
= 
（2）证明：连接AC．
∵ = ，
∴∠BAC=∠ACD，
∵OA=OC，
∴∠OAC=∠OCA，
∴∠BAO=∠OCD，
∵PQ∥AB，
∴∠BAO=∠APQ，
∴∠COD=∠APQ
（3）连接AD、AH、BP、BQ、DP，延长CO交PQ于M，作AN⊥BD于N．
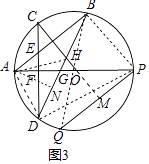
∵∠OCD=∠APQ．OC=OP，∠AOC=∠POM，
∴△COF≌△POM，
∴CF=PM，
∵PQ=2CF，
∴PQ=2PM，
∴M是PQ的中点，
∴OM⊥PQ，
∴∠CFO=∠PMO=90°
∴AP⊥CD，
∴ = ，
PQ∥AB，
∴∠OMP=∠AKM=90°，
∴OC⊥AB，
∴ = ，
∴AK=BK，
∴ = = ，OC垂直平分AB，设GH=a，
∴BH=5GH=5a，
∵OC垂直平分AB，
∴AH=BH=5a，∠HAB=∠HBA，
∴∠AHD=2∠ABH，
∵ = = ，
∴∠ADC=∠CDB=∠ABD，
∴∠ADH=2∠ADC=2∠ABH=∠AHD，
∴AH=AD=5a，
∵CD⊥AP，
∴∠AFD=∠GFD=90°，
∵DF=DF，∠ADC=∠CDB，
∴△ADF≌△GDF，
∴AD=DG=5a，
∴DH=6a，BD=11a，
∵AH=AD，AN⊥DH，
∴NH= 
DH=3a，
AN= 
=4a，BN=BH+NH=8a，
在Rt△ABN中，
tan∠ABD= 
= 
= ，
∵ = ，
∴∠ABD=∠APD，
∴tan∠ABD=tan∠APD= ，
∵AP是直径，
∴∠ADP=90°，
∴ 
= ，
∴PD=2AD=10a，AP= 
=5 
a，
∵AP为直径，
∴∠ABP=90°，
∵PQ∥AB，
∴∠ABP+∠BPQ=180°，
∵∠ABP=90°，
∴∠BPQ=90°，
∴BQ为⊙O的直径，
∴BQ=5 a，
∵BQ为⊙O的直径，
∴∠BDQ=90°，
∴DQ= 
=2a，
∵DQ=4，
∴2a=4，
∴a=2，AP=5 a=10 ，
∴⊙O的半径OA= AP=5
【解析】（1）连接AD、BC，只要证明△AED≌△CEB，即可解决问题．（2）连接AC．想办法证明：∠OCD、∠APQ都与∠PAB相等即可．（3）连接AD、AH、BP、BQ、DP，延长CO交PQ于M，作AN⊥BD于N．由△COF≌△POM，推出M是PQ的中点，OC垂直平分AB，设GH=a，则BH=5GH=5a，由OC垂直平分AB，推出AH=BH=5a，∠HAB=∠HBA，推出∠AHD=2∠ABH，由 = = ，推出∠ADC=∠CDB=∠ABD，推出∠ADH=2∠ADC=2∠ABH=∠AHD，推出AH=AD=5a，由△ADF≌△GDF，推出AD=DG=5a，推出DH=6a，BD=11a，由AH=AD，AN⊥DH，推出NH= DH=3a，AN= =4a，BN=BH+NH=8a，在Rt△ABN中， tan∠ABD= = = ，由 = ，推出∠ABD=∠APD，推出tan∠ABD=tan∠APD= ，推出 = ，推出PD=2AD=10a，AP= =5 a，再证明BQ为⊙O的直径，想办法列出方程即可解决问题．
