题目内容
【题目】如图,在△ABC中,AB=AC,CD垂直AB于D,P为BC上的任意一点,过P点分别作PE⊥AB,PF⊥CA,垂足分别为E,F.
(1)若P为BC边中点,则PE,PF,CD三条线段有何数量关系(写出推理过程)?
(2)若P为线段BC上任意一点,则(1)中关系还成立吗?
(3)若P为直线BC上任意一点,则PE,PF,CD三条线段间有何数量关系(请直接写出).
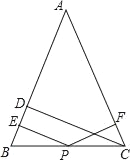
【答案】(1)CD=PE+PF,理由详见解析;(2)成立,理由详见解析;(3)PE﹣PF=CD或PF﹣PE=CD.
【解析】
(1)如图1,连接PA,根据三角形的面积公式列方程即可得到结论;
(2)连接PA,根据三角形的面积公式即可得到结论;
(3)如图2和图3,连接PA,根据三角形的面积列方程即可得到结论.
(1)CD=PE+PF.理由如下:
如图1,连接PA.
∵CD⊥AB于D,PE⊥AB于E,PF⊥AC于F.
∵S△ABC![]() AB×CD,S△PAB
AB×CD,S△PAB![]() AB×PE,S△PAC
AB×PE,S△PAC![]() AC×PF.
AC×PF.
又∵S△ABC=S△PAB+S△PAC,∴![]() AB×CD
AB×CD![]() AB×PE
AB×PE![]() AC×PF.
AC×PF.
∵AB=AC,∴CD=PE+PF.
(2)成立,理由如下:
连接PA.
∵CD⊥AB于D,PE⊥AB于E,PF⊥AC于F.
∵S△ABC![]() AB×CD,S△PAB
AB×CD,S△PAB![]() AB×PE,S△PAC
AB×PE,S△PAC![]() AC×PF.
AC×PF.
又∵S△ABC=S△PAB+S△PAC,∴![]() AB×CD
AB×CD![]() AB×PE
AB×PE![]() AC×PF.
AC×PF.
∵AB=AC,∴CD=PE+PF.
(3)结论:PE﹣PF=CD或PF﹣PE=CD.理由如下:
如图2,连接PA.
∵CD⊥AB于D,PE⊥AB于E,PF⊥AC于F.
∵S△ABC![]() AB×CD,S△PAB
AB×CD,S△PAB![]() AB×PE,S△PAC
AB×PE,S△PAC![]() AC×PF.
AC×PF.
又∵S△ABC=S△PAC﹣S△PAB,∴![]() AB×CD
AB×CD![]() AC×PF
AC×PF![]() AB×PE.
AB×PE.
∵AB=AC,∴CD=PF﹣PE.
如图3,连接PA.
∵CD⊥AB于D,PE⊥AB于E,PF⊥AC于F.
∵S△ABC![]() AB×CD,S△PAB
AB×CD,S△PAB![]() AB×PE,S△PAC
AB×PE,S△PAC![]() AC×PF.
AC×PF.
又∵S△ABC=S△PAB﹣S△PAC,∴![]() AB×CD
AB×CD![]() AB×PE
AB×PE![]() AC×PF.
AC×PF.
∵AB=AC,∴CD=PE﹣PF.

 名校课堂系列答案
名校课堂系列答案