Question

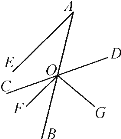
【题目】如图，O是直线AB上一点，∠COD＝90°，OE、OF分别是∠COB、∠AOD的平分线，且∠COB：∠AOD＝4：9．

（1）写出图中∠BOD的余角和补角；

（2）求∠AOC的度数

Answer 1

【答案】（1）∠BOD的余角为∠BOC，∠BOD的补角为∠AOD；（2）∠AOC＝108°．

【解析】

（1）依据∠COD＝90°，∠AOB＝180°，即可得到∠BOD的余角为∠BOC，∠BOD的补角为∠AOD；

（2）依据∠COB：∠AOD＝4：9，即可得到9（90°﹣∠BOD）＝4（180°﹣∠BOD），求得∠BOD＝18°，即可得到∠AOC的度数．

解：（1）∵∠COD＝90°，∠AOB＝180°，

∴∠BOC＝90°﹣∠BOD，∠AOD＝180°﹣∠BOD，

即∠BOD的余角为∠BOC，∠BOD的补角为∠AOD；

（2）∵∠COB：∠AOD＝4：9，且∠BOC＝90°﹣∠BOD，∠AOD＝180°﹣∠BOD，

∴9（90°﹣∠BOD）＝4（180°﹣∠BOD），

解得∠BOD＝18°，

∴∠BOC＝90°﹣18°＝72°，

∴∠AOC＝180°﹣72°＝108°．