题目内容
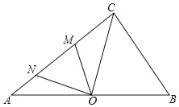
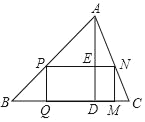
【题目】如图三角形ABC,BC=12,AD是BC边上的高AD=10.P,N分别是AB,AC边上的点,Q,M是BC上的点,连接PQMN,PN交AD于E.求
(1)若四边形PQMN是矩形,且PQ:PN=1:2.求PQ、PN的长;
(2)若四边形PQMN是矩形,求当矩形PQMN面积最大时,求最大面积和PQ、PN的长.

【答案】(1)PQ=![]() ,PN=
,PN=![]() ;(2)PQ=5,PN=6.
;(2)PQ=5,PN=6.
【解析】
(1)设PQ=y,则PN=2y,根据相似三角形的对应边上的高的比=相似比,构建方程即可解决问题;
(2)设AE=x.利用相似三角形的性质,用x表示PN,PQ,构建二次函数,利用二次函数的性质解决问题即可.
解:(1)设PQ=y,则PN=2y,
∵四边形PQMN是矩形,
∴PN∥BC,
∴△APN∽△ABC,
∵AD⊥BC,
∴AD⊥PN,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
解得y=![]() ,
,
∴PQ=![]() ,PN=
,PN=![]() .
.
(2)设AE=x.
∵四边形PQMN是矩形,
∴PN∥BC,
∴△APN∽△ABC,
∵AD⊥BC,
∴AD⊥PN,
∴![]() =
=![]() ,
,
∴PN=![]() x,PQ=DE=10﹣x,
x,PQ=DE=10﹣x,
∴S矩形PQMN=![]() x(10﹣x)=﹣
x(10﹣x)=﹣![]() (x﹣5)2+30,
(x﹣5)2+30,
∴当x=5时,S的最大值为30,
∴当AE=5时,矩形PQMN的面积最大,最大面积是30,
此时PQ=5,PN=6.

练习册系列答案
相关题目