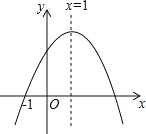��Ŀ����
����Ŀ����ͼ����ƽ��ֱ������ϵ�У����κ�����ͼ����������A(-1��0)��B(4��0)��C(0��-4)���㣬��P��ֱ��BC�·���������һ���㣮
��1��д��������κ����Ľ���ʽ��
��2���Ƿ���ڵ�P��ʹ��POC����OCΪ�ױߵĵ��������Σ������ڣ����P�����ꣻ�����ڣ���˵�����ɣ�
��3������P��x��Ĵ��ߣ���ֱ��BC�ڵ�E������P�˶���ʲôλ��ʱ���߶�PE��ֵ��������ʱP�����꣮
���𰸡���1��![]() ����2�����ڣ�(
����2�����ڣ�(![]() ����2)����3����m=2ʱ��PE��ֵ���ʱP������Ϊ(2��-6)
����2)����3����m=2ʱ��PE��ֵ���ʱP������Ϊ(2��-6)
��������
��1������֪�ĵ��������뺯������ʽ�����ô���ϵ����ֱ����⣮
��2�����á�POC����OCΪ�ױߵĵ��������Σ�����![]() ������P��OC�Ĵ�ֱƽ�����ϣ���P��ֱ��BC�·��������ϣ�����P�Ǵ�ֱƽ�����������ߵĽ��㣬ͨ���ⷽ�̵õ��𰸣�
������P��OC�Ĵ�ֱƽ�����ϣ���P��ֱ��BC�·��������ϣ�����P�Ǵ�ֱƽ�����������ߵĽ��㣬ͨ���ⷽ�̵õ��𰸣�
��3������P��x��Ĵ��ߣ���BC��E�����P�����꣬��֪E�ĺ�������P�ĺ�������ͬ������ֱ��BC�Ľ���ʽ��ʾE�������꣬��PE��![]() ����������ϵʽ�����ö��κ��������������ֵ���ɣ�
����������ϵʽ�����ö��κ��������������ֵ���ɣ�
�⣺��1����������Ϊ��![]()
��A(-1��0)��B(4��0)��C(0��-4)����ã�
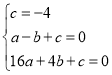 ��ã�
��ã�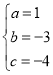
���������߽���ʽΪ![]()
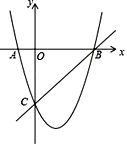
��2����OC�Ĵ�ֱƽ����DP��
��OC�ڵ�D����BC�·�
�������ڵ�P����ͼ1��
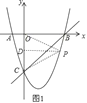
��PO=PD��
��ʱP�㼴Ϊ���������ĵ㣬
��C��0��-4����
��D��0����2����
��P����������2��
���������߽���ʽ�ɵ�![]() ��
��
���![]() ��С��0����ȥ����
��С��0����ȥ����
���������������P�㣬
��������![]() ����2��
����2��
��3���ߵ�P���������ϣ�
����P��m��m2-3m-4��
��B��4��0����C��0��-4��
����ֱ��B C�Ľ���ʽΪ��y=x-4
���E������m��m-4��
��PE= (m-4)-( m2-3m-4)
=-m2+4m
=-(m-2)2+4
��-1<0
�൱m=2ʱ��PE��ֵ���
��ʱP������Ϊ��2��-6��