题目内容
【题目】如图,直线y=﹣2x+4与坐标轴分别交于C、B两点,过点C作CD⊥x轴,点P是x轴下方直线CD上的一点,且△OCP与△OBC相似,求过点P的双曲线解析式.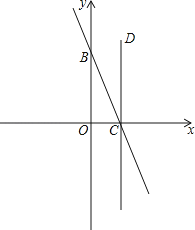
【答案】解:∵直线y=﹣2x+4与坐标轴分别交于C、B两点,
∴令y=0,可得﹣2x+4=0,解得x=2,即C(2,0),OC=2,
令x=0,可得y=4,即B(0,4),OB=4,
①如图1,当∠OBC=∠COP时,△OCP∽△BOC,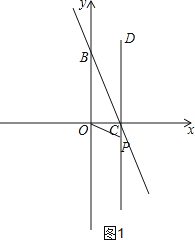
∴![]() =
=![]() ,即
,即![]() =
=![]() ,解得CP=1,
,解得CP=1,
∴P(2,﹣1),
设过点P的双曲线解析式y=![]() ,把P点代入解得k=﹣2,
,把P点代入解得k=﹣2,
∴过点P的双曲线解析式y=﹣![]() ,
,
②如图2,当∠OBC=∠CPO时,△OCP∽△COB,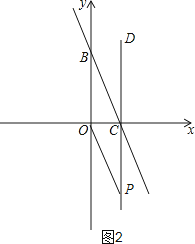
在△OCP和△COB中,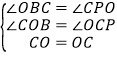
∴△OCP≌△COB(AAS)
∴CP=BO=4,
∴P(2,﹣4)
设过点P的双曲线解析式y=![]() ,把P点代入得﹣4=
,把P点代入得﹣4=![]() ,解得k=﹣8,
,解得k=﹣8,
∴过点P的双曲线解析式y=![]() .
.
综上可得,过点P的双曲线的解析式为y=﹣![]() 或y=
或y=![]() .
.
【解析】由直线y=﹣2x+4与坐标轴分别交于C、B两点,易得OC=2,OB=4,再分两种情况①当∠OBC=∠COP时,△OCP与△OBC相似,②当∠OBC=∠CPO时,△OCP与△OBC相似分别求出点的坐标,再求出过点P的双曲线解析式.
【考点精析】解答此题的关键在于理解相似三角形的判定与性质的相关知识,掌握相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.

练习册系列答案
相关题目