题目内容
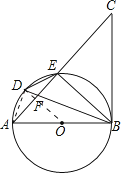
【题目】如图,AB是⊙O的直径,点D是![]() 上一点,且∠BDE=∠CBE,BD与AE交于点F.
上一点,且∠BDE=∠CBE,BD与AE交于点F.
(1)求证:BC是⊙O的切线。
(2)若BD平分∠ABE,求证:DE2=DFDB。
(3)在(2)的条件下,延长ED,BA交于点P,若PA=AO,DE=2,求PD的长和⊙O的半径。
【答案】
(1)
证明:∵AB是⊙O的直径,
∴∠AEB=90°,
∴∠EAB+∠EBA=90°,
∵∠EDB=∠EAB,∠BDE=∠CBE,
∴∠EAB=∠CBE,
∴∠ABE+∠CBE=90°,
∴CB⊥AB,
∵AB是⊙O的直径,
∴BC是⊙O的切线。
(2)
证明:∵BD平分∠ABE,
∴∠ABD=∠DBE,![]() =
=![]() ,
,
∴∠DEA=∠DBE,
∵∠EDB=∠BDE,
∴△DEF∽△DBE,
∴![]() =
=![]() ,
,
∴DE2=DFDB。
(3)
解:连接DA、DO,
∵OD=OB,
∴∠ODB=∠OBD,
∵∠EBD=∠OBD,
∴∠EBD=∠ODB,
∴OD∥BE,
∴![]() =
=![]() ,
,
∵PA=AO,
∴PA=AO=OB,
∴![]() =
=![]()
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∵DE=2,
∴PD=4,
∵∠PDA+∠ADE=180°,∠ABE+∠ADE=180°,
∴∠PDA=∠ABE,
∵OD∥BE,
∴∠AOD=∠ABE,
∴∠PDA=∠AOD,
∵∠P=∠P,
∴△PDA∽△POD,
∴![]() =
=![]() ,
,
设OA=x,
∴PA=x,PO=2x,
∴![]() =
=![]() ,
,
∴2x2=16,x=2![]() ,
,
∴OA=2![]() .
.
【解析】(1)根据圆周角定理即可得出∠EAB+∠EBA=90°,再由已知得出∠ABE+∠CBE=90°,则CB⊥AB,从而证得BC是⊙O的切线;
(2)通过证得△DEF∽△DBE,得出相似三角形的对应边成比例即可证得结论.
(3)连接DA、DO,先证得OD∥BE,得出![]() =
=![]() , 然后根据已知条件得出
, 然后根据已知条件得出![]() =
=![]() =
=![]() =
=![]() , 求得PD=4,通过证得△PDA∽△POD,得出
, 求得PD=4,通过证得△PDA∽△POD,得出![]() =
=![]() , 设OA=x,则PA=x,PO=2x,得出
, 设OA=x,则PA=x,PO=2x,得出![]() =
=![]() , 解得OA=2
, 解得OA=2![]() .
.
此题考查了圆的综合应用,涉及知识点有圆周角定理,切线的证明,相似三角形对应边成比例等。







