Question

【题目】如图，在平行四边形ABCD中，若AB=6，AD=10，∠ABC的平分线交AD于点E，交CD的延长线于点F，求DF的长．

Answer 1

【答案】解：∵四边形ABCD为平行四边形，
∴AB=DC=6，AD=BC=10，AB∥DC．
∵AB∥DC，
∴∠1=∠3，
又∵BF平分∠ABC，
∴∠1=∠2，
∴∠2=∠3，
∴BC=CF=10，
∴DF=CF﹣DC=10﹣6=4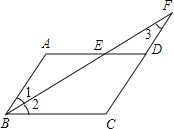

【解析】首先根据平行四边形的性质可得AB=DC=6，AD=BC=10，AB∥DC，再根据平行线的性质与角平分线的性质证明∠2=∠3，根据等角对等边可得BC=CF=10，再用CF﹣CD即可算出DF的长．
【考点精析】本题主要考查了平行四边形的性质的相关知识点，需要掌握平行四边形的对边相等且平行；平行四边形的对角相等，邻角互补；平行四边形的对角线互相平分才能正确解答此题．