题目内容
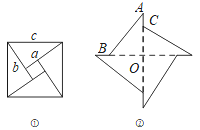
【题目】如图①,美丽的弦图,蕴含着四个全等的直角三角形.已知每个直角三角形较长的直角边为a,较短的直角边为b,斜边长为c.如图②,现将这四个全图②等的直角三角形紧密拼接,形成飞镖状,已知外围轮廓(实线)的周长为24,OC=3,则该飞镖状图案的面积( )
A. 6 B. 12 C. 24 D. 24![]()
【答案】C
【解析】
根据飞镖状图案的周长求出AB+AC的长,在直角三角形AOB中,利用勾股定理求出AC的长,进而确定出OA的长,求出三角形AOB面积,即可确定出所求.
根据题意得:4(AB+AC)=24,即AB+AC=6,OB=OC=3,
在Rt△AOB中,根据勾股定理得:AB2=OA2+OB2,
即(6-AC)2=32+(3+AC)2,
解得:AC=1,
∴OA=3+1=4,
∴S△AOB=![]() ×3×4=6,
×3×4=6,
则该飞镖状图案的面积为24,
故选C.

练习册系列答案
相关题目










