题目内容
【题目】如图，抛物线y＝ax2+bx+c（a＜0）与x轴交于点A（﹣2，0）、B（4，0），与y轴交于点C，且OC＝2OA．
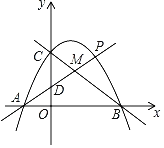
（1）该抛物线的解析式为 ；
（2）直线y＝kx+l（k＞0）与y轴交于点D，与直线BC交于点M，与抛物线上直线BC上方部分交于点P，设m＝
，求m的最大值及此时点P的坐标；
（3）若点D、P为（2）中求出的点，点Q为x轴的一个动点，点N为坐标平面内一点，当以点P、D、Q、N为顶点的四边形为矩形时，直接写出点N的坐标．
【答案】（1）y＝﹣
x2+x+4；（2）当n＝2时，m有最大值，最大值为
，此时P（2，4）；（3）满足条件的点N坐标为（
，3）或（6，﹣3）．
【解析】
（1）因为抛物线y=ax2+bx+c经过A（-2，0）、B（4，0）两点，所以可以假设y=a（x+2）（x-4），求出点C坐标代入求出a即可；
（2）由△CMD∽△FMP，可得
，根据m关于n的二次函数，利用二次函数的性质即可解决问题；
（3）存在这样的点Q、N，使得以P、D、Q、N四点组成的四边形是矩形．分两种情形讨论：①当DP是矩形的边时，有两种情形；②当DP是对角线时，利用相似三角形的性质和勾股定理可求解．
（1）因为抛物线y＝ax2+bx+c经过A（﹣2，0）、B（4，0）两点，
所以可以假设y＝a（x+2）（x﹣4），
∵OC＝2OA，OA＝2，
∴C（0，4），代入抛物线的解析式得到a＝﹣，
∴y＝﹣（x+2）（x﹣4）＝﹣x2+x+4，
故答案为：y＝﹣x2+x+4；
（2）如图1中，由题意，点P在y轴的右侧，作PE⊥x轴于E，交BC于F．
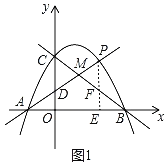
∵CD∥PE，
∴△CMD∽△FMP，
∴m＝
，
∵直线y＝kx+1（k＞0）与y轴交于点D，则D（0，1），
∵BC的解析式为y＝﹣x+4，
设P（n，﹣n2+n+4），则F（n，﹣n+4），
∴PF＝﹣n2+n+4﹣（﹣n+4）＝﹣（n﹣2）2+2，
∴m＝
＝﹣
（n﹣2）2+，
∵﹣＜0，
∴当n＝2时，m有最大值，最大值为，此时P（2，4）；
（3）存在这样的点Q、N，使得以P、D、Q、N四点组成的四边形是矩形．
①当DP是矩形的边时，有两种情形，
a、如图2﹣1中，四边形DQNP是矩形时，
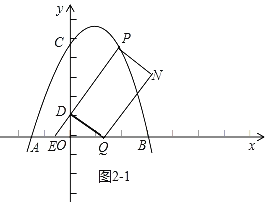
有（2）可知P（2，4），代入y＝kx+1中，得到k＝
，
∴直线DP的解析式为y＝x+1，可得D（0，1），E（﹣，0），
由△DOE∽△QOD可得
，
∴OD2＝OEOQ，
∴1＝OQ，
∴OQ＝，
∴Q（，0）．
根据矩形的性质，将点P向右平移个单位，向下平移1个单位得到点N，
∴N（2+，4﹣1），即N（，3）
b、如图2﹣2中，四边形PDNQ是矩形时，
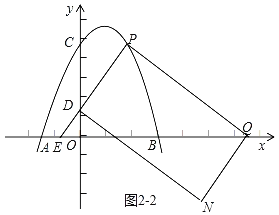
∵直线PD的解析式为y＝x+1，PQ⊥PD，
∴直线PQ的解析式为y＝﹣x+
，
∴Q（8，0），
根据矩形的性质可知，将点D向右平移6个单位，向下平移4个单位得到点N，
∴N（0+6，1﹣4），即N（6，﹣3）．
②当DP是对角线时，设Q（x，0），则QD2＝x2+1，QP2＝（x﹣2）2+42，PD2＝13，
∵Q是直角顶点，
∴QD2+QP2＝PD2，
∴x2+1+（x﹣2）2+16＝13，
整理得x2﹣2x+4＝0，方程无解，此种情形不存在，
综上所述，满足条件的点N坐标为（，3）或（6，﹣3）．
