Question

【题目】如图，一海轮位于灯塔P的西南方向，距离灯塔40了2海里的A处，它沿正东方向航行一段时间后，到达位于灯塔P的南偏东60°方向上的B处，求航程AB的值(结果保留根号).

Answer 1

【答案】海里

【解析】试题分析：过P作PC垂直于AB，在直角三角形ACP中，利用锐角三角函数定义求出AC与PC的长，在直角三角形BCP中，利用锐角三角函数定义求出CB的长，由AC+CB求出AB的长即可．

试题解析：

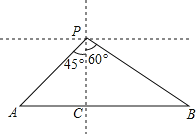
过P作PC⊥AB于点C，

在Rt△ACP中,PA=海里,∠APC=45°,sin∠APC=,cos∠APC=，

∴AC=APsin45°=×=40(海里),PC=APcos45°=×=40(海里)，

在Rt△BCP中,∠BPC=60°,tan∠BPC=，

∴BC=PCtan60°= (海里)，

则AB=AC+BC=(40+)海里。