题目内容
 如图,在菱形ABCD中,DE⊥AB,sinA=
如图,在菱形ABCD中,DE⊥AB,sinA=| 4 |
| 5 |
分析:设DE=4x,则AD=5x,AE=3x,BE=2x,结合BE=2,可得出x的值,继而可得出tan∠BDE的值.
解答:解:由题意得,sinA=
,四边形ABCD是菱形,
设DE=4x,则AD=5x,AE=3x,BE=2x,
∵BE=2,
∴x=1,
∴DE=4,
在Rt△BDE中,tan∠BDE=
=
.
故选A.
| 4 |
| 5 |
设DE=4x,则AD=5x,AE=3x,BE=2x,
∵BE=2,
∴x=1,
∴DE=4,
在Rt△BDE中,tan∠BDE=
| BE |
| DE |
| 1 |
| 2 |
故选A.
点评:此题考查了菱形的性质及解直角三角形的知识,解答本题的关键是根据四边相等的性质,利用方程思想得出各边长度,难度一般.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
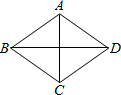 如图:在菱形ABCD中,AC=6,BD=8,则菱形的边长为( )
如图:在菱形ABCD中,AC=6,BD=8,则菱形的边长为( )| A、5 | B、10 | C、6 | D、8 |
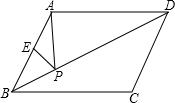
 ME交射线CD于点N,连接MD、AN.
ME交射线CD于点N,连接MD、AN. 如图,在菱形ABCD中,AE⊥BC,垂足为F,EC=1,∠B=30°,求菱形ABCD的周长.
如图,在菱形ABCD中,AE⊥BC,垂足为F,EC=1,∠B=30°,求菱形ABCD的周长.