题目内容
【题目】已知![]() 是边长为
是边长为![]() 的等边三角形,动点
的等边三角形,动点![]() 以
以![]() 的速度从点
的速度从点![]() 出发,沿线段
出发,沿线段![]() 向点
向点![]() 运动.
运动.
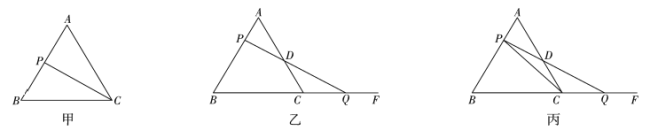
(1)如图甲,设点![]() 的运动时间为
的运动时间为![]() ,那么
,那么![]() 为何值时,
为何值时,![]() 是直角三角形?
是直角三角形?
(2)若另一动点![]() 从点
从点![]() 出发,沿射线
出发,沿射线![]() 方向运动,连接
方向运动,连接![]() 交
交![]() 于点
于点![]() ,如果动点
,如果动点![]() 都以
都以![]() 的速度同时出发.
的速度同时出发.
①如图乙,设运动时间为![]() ,那么
,那么![]() 为何值时,
为何值时,![]() 是等腰三角形?
是等腰三角形?
②如图丙,连接![]() ,请你猜想:在点
,请你猜想:在点![]() 的运动过程中,
的运动过程中,![]() 和
和![]() 的面积有什么关系?并说明理由.
的面积有什么关系?并说明理由.
【答案】(1)![]() ;(2)①t=1;②相等,理由见解析
;(2)①t=1;②相等,理由见解析
【解析】
(1)当△PBC是直角三角形时,∠B=60°,所以BP=1.5cm,即可算出t的值;
(2)①因为∠DCQ=120°,当△DCQ是等腰三角形时,CD=CQ,然后可证明△APD是直角三角形,即可根据题意求出t的值;②面积相等.可通过同底等高验证.
解:(1)∵![]() 是等边三角形,∴
是等边三角形,∴![]() .
.
当![]() 是直角三角形时,
是直角三角形时,![]() ,
,![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∴![]()
(2)①![]() 是等边三角形,
是等边三角形,
∴![]() ,∴
,∴![]() ,
,
当![]() 是等腰三角形时,
是等腰三角形时,![]() ,
,
∴![]()
又∵![]() ,∴
,∴![]() ,
,
∴![]()
∵![]() ,即
,即![]() ,
,
∴![]()
②相等
理由如下:如图,
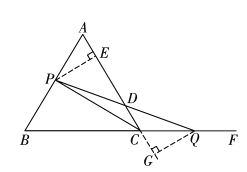
过点![]() 作
作![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 的延长线于点
的延长线于点![]() ,
,
∵![]() ,
,![]() ,∴
,∴![]()
∵![]() ,
,![]() ,
,
∴![]()
在![]() 和
和![]() 中,
中,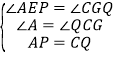 ,
,
∴![]()
∴![]() ,
,
∴![]() 和
和![]() 同底等高,
同底等高,
∴![]() 和
和![]() 的面积相等.
的面积相等.

练习册系列答案
相关题目