题目内容
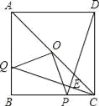
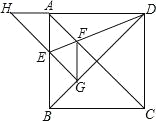
【题目】如图,正方形ABCD的边长为1,AC,BD是对角线。将△DCB绕着点D顺时针旋转45°得到△DGH,HG交AB于点E,连接DE交AC于点F,连接FG。则下列结论:①四边形AEGF是菱形;②△AED≌△GED;③∠DFG=112.5°;④BC+FG=1.5.其中正确的结论是( )
A. ①②③④ B. ①②③ C. ①② D. ②
【答案】B
【解析】
首先证明△ADE≌△GDE,再求出∠AEF、∠AFE、∠GEF、∠GFE的度数,推出AE=EG=FG=AF,由此可以一一判断.
解:∵四边形ABCD是正方形,
∴AD=DC=BC=AB,∠DAB=∠ADC=∠DCB=∠ABC=90°,∠ADB=∠BDC=∠CAD=∠CAB=45°,
∵△DGH是由△DCB旋转得到,
∴DG=DC=AD,∠DGE=∠DCB=∠DAE=90°,
在Rt△AED和Rt△GED中,
![]()
∴△AED≌△GED,故②正确,
∴∠ADE=∠EDG=22.5°,AE=GE,
∴∠AED=∠AFE=67.5°,
∴AE=AF,同理GE=GF,
∴AE=GE=GF=AF,
∴四边形AEGF是菱形,故①正确,
∵∠DFG=∠GFC+∠DFC=∠BAC+∠DAC+∠ADF=112.5°,故③正确.
∵AE=FG=EG=BG,BE=![]() AE,
AE,
∴BE>AE,
∴AE<![]() ,
,
∴CB+FG<1.5,故④错误.
故选:B

练习册系列答案
相关题目