Question

如图，已知抛物线与x轴相交于A、B两点，与y轴相交于点C，若已知A点的坐标为A（﹣2，0）．

（1）求抛物线的解析式及它的对称轴方程；
（2）求点C的坐标，连接AC、BC并求线段BC所在直线的解析式；
（3）试判断△AOC与△COB是否相似？并说明理由；
（4）在抛物线的对称轴上是否存在点Q，使△ACQ为等腰三角形？若不存在，求出符合条件的Q点坐标；若不存在，请说明理由．

Answer 1

解：（1）∵抛物线的图象经过点A（﹣2，0），
∴，解得：。
∴抛物线解析式为。
又∵，
∴对称轴方程为：x=3。
（2）在中，令x=0，得y=4，∴C（0，4）；
令y=0，即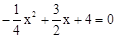，整理得x²﹣6x﹣16=0，解得：x=8或x=﹣2。
∴A（﹣2，0），B（8，0）。
设直线BC的解析式为y=kx+b，
把B（8，0），C（0，4）的坐标分别代入解析式，得：
，解得。
∴直线BC的解析式为：。
（3）可判定△AOC∽△COB成立。理由如下：
在△AOC与△COB中，∵OA=2，OC=4，OB=8，∴。
又∵∠AOC=∠BOC=90°，∴△AOC∽△COB。
（4）存在。
∵抛物线的对称轴方程为：x=3，∴可设点Q（3，t），则可求得：
。
①当AQ=CQ时，有，即25+t²=t²﹣8t+16+9，解得t=0。
∴Q₁（3，0）。
②当AC=AQ时，有，即t²=﹣5，此方程无实数根，
∴此时△ACQ不能构成等腰三角形。
③当AC=CQ时，有，整理得：t²﹣8t+5=0，解得：。
∴点Q坐标为：Q₂（3，），Q₃（3，）。
综上所述，存在点Q，使△ACQ为等腰三角形，点Q的坐标为：Q₁（3，0），Q₂（3，），Q₃（3，）

解析