��Ŀ����
��2013���Ĵ�����12�֣���ͼ�����κ���y=ax2+bx+c��ͼ��Ķ���C������Ϊ��0����2������x����A��B���㣬����A����1��0����ֱ��l��x=m��m��1����x�ύ��D��
��1������κ����Ľ���ʽ��B�����ꣻ
��2����ֱ��l���ҵ�P��P�ڵ�һ���ޣ���ʹ����P��D��BΪ���������������B��C��OΪ��������������ƣ����P�����꣨�ú�m�Ĵ���ʽ��ʾ����
��3���ڣ�2�������������£������������Ƿ���ڵ�һ�����ڵĵ�Q��ʹ��BPQ����PΪֱ�Ƕ���ĵ���ֱ�������Σ�������ڣ��������Q�����ꣻ��������ڣ���˵�����ɣ�
�⣺��1����������y=ax2+bx+c�Ķ�������ΪC��0����2������b=0��c=��2��
��y=ax2+bx+c����A����1��0������0=a+0��2��a=2��
�������ߵĽ���ʽΪy=2x2��2��
��y=0ʱ��2x2��2=0�����x=��1��
���B��������1��0����
��2����P��m��n����
�ߡ�PDB=��BOC=90�㣬
�൱��P��D��BΪ���������������B��C��OΪ���������������ʱ�������������
������OCB�ס�DBP���� ����
����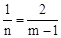 �����
�����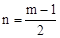 ��
��
�ɶԳ��Կ�֪����x���Ϸ����·�����һ������������
���ʱ��P����Ϊ��m�� ����m��
����m�� ����
����
������OCB�ס�DPB���� ����
����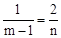 �����n=2m��2��
�����n=2m��2��
�ɶԳ��Կ�֪����x���Ϸ����·�����һ������������
���ʱ��P����Ϊ��m��2m��2����m��2��2m����
�������������������ĵ�P������Ϊ����m�� ������m��
������m�� ������m��2m��2����m��2��2m����
������m��2m��2����m��2��2m����
��3���������������ϴ��ڵ�һ�����ڵĵ�Q��x��2x2��2����ʹ��BPQ����PΪֱ�Ƕ���ĵ���ֱ�������Σ�
��ͼ������Q��QE��l�ڵ�E��
�ߡ�DBP+��BPD=90�㣬��QPE+��BPD=90�㣬
���DBP=��QPE��
�ڡ�DBP���EPQ�У��� ��
��
���DBP�ա�EPQ����BD=PE��DP=EQ��
�����������
�ٵ�P��m�� ��ʱ��
��ʱ��
��B��1��0����D��m��0����E��m��2x2��2����
�� �����
����� ��
�� ��������������ȥ����
��������������ȥ����
�ڵ�P��m��2m��2��ʱ��
��B��1��0����D��m��0����E��m��2x2��2����
��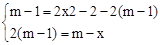 �����
����� ��
�� ��������������ȥ����
��������������ȥ����
�������������������������ĵ�Q��
����

 �Ͻ�ƽСѧ��������ϵ�д�
�Ͻ�ƽСѧ��������ϵ�д�ij�̳���Ӫij��Ʒ�Ƶ���ߣ�����ʱ�ĵ�����30Ԫ�������г����飺��һ��ʱ���ڣ����۵�����40Ԫʱ����������600���������۵���ÿ��1Ԫ���ͻ����۳�10����ߣ�
��1�����������Ʒ����ߵ����۵���ΪxԪ��x��40��������ֱ���x�Ĵ���ʽ����ʾ������y�������۸�Ʒ����������wԪ�����ѽ����д�ڱ����У�
| ���۵��ۣ�Ԫ�� | x |
| ������y������ | �������� |
| ������������w��Ԫ�� | �������� |
��3���ڣ�1���������£�����߳��涨��Ʒ��������۵��۲�����44Ԫ�����̳�Ҫ��ɲ�����540���������������̳����۸�Ʒ�����õ���������Ƕ��٣�
��2013���㽭����10�֣�Ϊӭ���й�ɭ���ᣬij�̼Ҽƻ��ӳ��Ҳɹ�A��B���ֲ�Ʒ��20������Ʒ�IJɹ����ۣ�Ԫ/�����Dzɹ�������������һ�κ������±��ṩ�˲��ֲɹ����ݣ�
| �ɹ����������� | 1 | 2 | �� |
| A��Ʒ���ۣ�Ԫ/���� | 1480 | 1460 | �� |
| B��Ʒ���ۣ�Ԫ/���� | 1290 | 1280 | �� |
��2�����̼��볧��Э�̣��ɹ�A��Ʒ������������B��Ʒ������
 ����A��Ʒ�ɹ����۲�����1200Ԫ������̼ҹ��м��ֽ���������
����A��Ʒ�ɹ����۲�����1200Ԫ������̼ҹ��м��ֽ�����������3�����̼ҷֱ���1760Ԫ/����1700Ԫ/�������۵����۳�A��B���ֲ�Ʒ����ȫ�����꣮�ڣ�2���������£���ɹ�A�ֲ�Ʒ���ټ�ʱ������������������
 ��������ֱ��ڵ�A��B����ֱ��y=x���ڵ�C�����߶�OA�ϣ�����Q��ÿ��1����λ���ȵ��ٶȴӵ�O�������A�������˶���ͬʱ����P�ӵ�A�������O�������˶�������P��Q����һ��ֹͣ�˶�ʱ����һ��Ҳֹͣ�˶����ֱ����P��Q��x��Ĵ��ߣ���ֱ��AB��OC�ڵ�E��F������EF�����˶�ʱ��Ϊt�룬���˶��������ı���PEFQ��Ϊ���Σ���P��Q�غϳ��⣩��
��������ֱ��ڵ�A��B����ֱ��y=x���ڵ�C�����߶�OA�ϣ�����Q��ÿ��1����λ���ȵ��ٶȴӵ�O�������A�������˶���ͬʱ����P�ӵ�A�������O�������˶�������P��Q����һ��ֹͣ�˶�ʱ����һ��Ҳֹͣ�˶����ֱ����P��Q��x��Ĵ��ߣ���ֱ��AB��OC�ڵ�E��F������EF�����˶�ʱ��Ϊt�룬���˶��������ı���PEFQ��Ϊ���Σ���P��Q�غϳ��⣩��
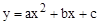 ����A��B��C���㣬����ΪF��
����A��B��C���㣬����ΪF��
 ��x���ཻ��A��B���㣬��y���ཻ�ڵ�C������֪A�������ΪA����2��0����
��x���ཻ��A��B���㣬��y���ཻ�ڵ�C������֪A�������ΪA����2��0����


 ��
��