题目内容
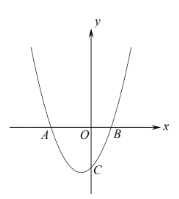
【题目】已知如图，抛物线
交
轴于
两点(
点在
点的左侧)，交
轴于点
.已知
．
（1）求抛物线的解析式；
（2）已知直线
，若直线与抛物线有且只有一个交点
求
的面积；
（3）在（2）的条件下，抛物线上是否存在点
使
若存在，请直接写出点
的坐标；若不存在，请说明理由．
【答案】（1）
；（2）
；（3）存在，
．
【解析】
（1）先求出点
的坐标，进而求出点
，
坐标，最后用待定系数法即可得出结论；
（2）联立直线
与抛物线的解析式得出一元二次方程，判别式为0，求出点
坐标，即可得出结论；
（3）Ⅰ、当点
在
轴上方时，先构造出
，进而求出点
的坐标，再联立直线
与抛物线的解析式，解方程组即可得出点坐标，
Ⅱ、当点在轴下方时，判断出点
和点关于轴对称，进而联立直线
与抛物线的解析式，解方程组即可得出结论．
解：（1）对于抛物线
，
令
，则
，
，
，
，
，
，
，
，
点，在抛物线上，
，
，
抛物线的解析式为；
（2）由（1）知，抛物线的解析式为①，
直线②与抛物线有且只有一个交点，
联立①②得，
，
，
△
，
，
，
，
，
直线
的解析式为
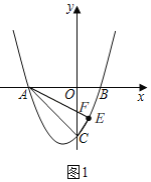
如图1，记直线与
轴的交点为
，则
，
；
（3）由（2）知，
，
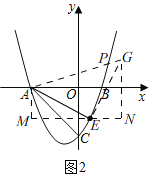
Ⅰ、当点在轴上方时，如图2，
将线段以点为旋转中心顺时针旋转
得到线段
，连接，则
，
在
中，
，
，
，
点是与抛物线的交点，
过点作
，过点作
于
，过点作
于，
，，
，
，
，
，
由旋转知，
，
，
，
，
，
，
，
，
，
，
，
直线的解析式为
③，
抛物线的解析式为④，
联立③④解得，
或
，
，
，
Ⅱ、由Ⅰ知，点的坐标为，，
，，
点与点关于轴对称，
点是直线与抛物线的交点，
，
直线的解析式为
⑤，
联立④⑤，解得，或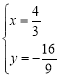
，
，
，即满足条件的点的坐标为
，或
，．
练习册系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
