Question

【题目】（1）如图1，三角形ABC中，BO平分∠ABC、CO平分∠ACB，则∠BOC与∠A的数量关系是 ；

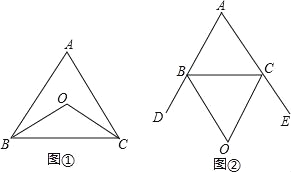
（2）如图2，BO平分△ABC的外角∠CBD、CO平分△ABC的外角∠BCE，则∠BOC与∠A的关系是 ；

（3）请就图2及图2中的结论进行证明．

Answer 1

【答案】（1）∠BOC=90°+∠A；（2）∠BOC=90°-∠A；（3）证明见解析.

【解析】

试题分析：（1）根据角平分线的定义可得∠OBC=∠ABC，∠OCB=∠ACB，然后表示出∠OBC+∠OCB，再根据三角形的内角和等于180°列式整理即可；

（2）由三角形的一个外角等于与它不相邻的两个内角的和可证2∠1+2∠2=2∠A+∠ABC+∠ACB=∠A+180°，再根据三角形内角和定理可证2∠BOC=180°-∠A，即∠BOC=90°-∠A；

（3）由三角形的一个外角等于与它不相邻的两个内角的和可证2∠1+2∠2=2∠A+∠ABC+∠ACB=∠A+180°，再根据三角形内角和定理可证2∠BOC=180°-∠A，即∠BOC=90°-∠A．

试题解析：（1）∠BOC=90°+∠A．

∵∠ABC与∠ACB的平分线相交于点O，

∴∠OBC=∠ABC，∠OCB=∠ACB，

∴∠OBC+∠OCB=（∠ABC+∠ACB），

在△OBC中，∠BOC=180°-（∠OBC+∠OCB）

=180°-（∠ABC+∠ACB）

=180°-

=90°+∠A，

（2）∠BOC与∠A的关系是∠BOC=90°-∠A．

（3）如图，

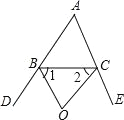
∵BO、CO分别是△ABC的外角∠DBC、∠ECB的角平分线，

∴∠DBC=2∠1=∠ACB+∠A，

∠ECB=2∠2=∠ABC+∠A，

∴2∠1+2∠2=2∠A+∠ABC+∠ACB=∠A+180°，

又∵∠1+∠2+∠BOC=180°，

∴2∠BOC=180°-∠A，

∴∠BOC=90°-∠A．