��Ŀ����
����Ŀ����ƽ��ֱ������ϵxOy�У�������G��y��mx2+2mx+m��1��m��0����y�ύ�ڵ�C��������G�Ķ���ΪD��ֱ�ߣ�y��mx+m��1��m��0����

��1����m��1ʱ������ֱ�ߺ�������G����ֱ��д��ֱ�߱�������G�صõ��߶γ���
��2������mȡֵ�ı仯���жϵ�C��D�Ƿ���ֱ���ϲ�˵�����ɣ�
��3����ֱ�߱�������G�صõ��߶γ���С��2����Ϻ�����ͼ��ֱ��д��m��ȡֵ��Χ��
���𰸡���1������������2������mȡ��ֵ����C��D����ֱ���ϣ�����������3��m��ȡֵ��Χ��m�ܩ�![]() ��m��
��m��![]() ��
��
��������
��1����m��1ʱ��������G�ĺ�������ʽΪy��x2+2x��ֱ�ߵĺ�������ʽΪy��x�����ֱ�߱�������G�صõ��߶Σ��ٻ�������������ͼ�ɣ�
��2�������C��D��������꣬�ٴ���ֱ�ߵĽ���ʽ���м��鼴�ɣ�
��3��������ֱ���������ߵĽ���ʽ��������ǵĽ������꣬�ٸ�������������֮��ľ��벻С��2�г�����ʽ����⼴�ɣ�
��1����m=1ʱ��������G�ĺ�������ʽΪy=x2+2x��ֱ�ߵĺ�������ʽΪy=x��
ֱ�߱�������G�صõ��߶γ�Ϊ![]() ��
��
����������������ͼ����ͼ��ʾ��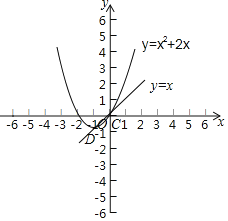
��2������mȡ��ֵ����C��D����ֱ���ϣ��������£�
��������G��y=mx2+2mx+m-1��m��0����y�ύ�ڵ�C��
���C������ΪC��0��m-1����
��y=mx2+2mx+m-1=m��x+1��2-1��
��������G�Ķ���D������Ϊ��-1��-1����
����ֱ�ߣ�y=mx+m-1��m��0����
��x=0ʱ��y=m-1��
��x=-1ʱ��y=m����-1��+m-1=-1��
������mȡ��ֵ����C��D����ֱ���ϣ�
��3���ⷽ����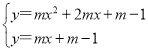 ��
��
��![]() ����
����![]() ��
��
��ֱ����������G�Ľ���Ϊ��0��m-1������-1��-1����
��ֱ�߱�������G�صõ��߶γ���С��2��
��![]() ��2��
��2��
��1+m2��4��m2��3��
��m��-![]() ��m��
��m��![]()
��
��m��ȡֵ��Χ��m��-![]() ��m��
��m��![]() ��
��

 ��У����ϵ�д�
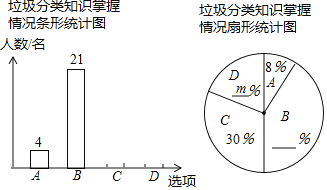
��У����ϵ�д�����Ŀ��Ϊ������Ӧ�����ﴫͳ�Ļ����ĺ��٣�ijѧУ����ȫУ1200��ѧ�����о���ʫ���б�������ڻ֮��ٰ쾭��ʫ�ʴ�����Ϊ�˽Ȿ��ϵ�л�ij���Ч����ѧУ��ί�ڻ����֮���������ȡ����ѧ��������һ��ʫ���б��������������������Ƴɵ�ͳ��ͼ�����֣���ͼ��ʾ��
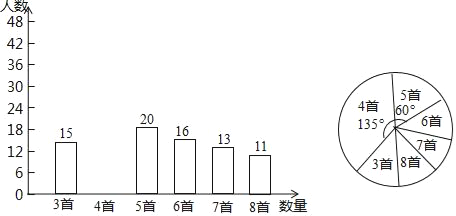
����������һ���£��ٴγ���ⲿ��ѧ����һ��ʫ���б������������Ƴ�ͳ�Ʊ�
һ��ʫ���б����� | 3�� | 4�� | 5�� | 6�� | 7�� | 8�� |
���� | 10 | 10 | 15 | 40 | 25 | 20 |
����ݵ������Ϣ
��1�������֮��ѧ����һ��ʫ���б�����������λ��Ϊ������
��2�����ƴ�����һ���¸�Уѧ��һ��ʫ���б�6�ף���6�ף����ϵ�������
��3��ѡ���ʵ���ͳ��������������ͬ�ĽǶȷ������ε����������ݣ����۸�У����ʫ���б�ϵ�л��Ч����
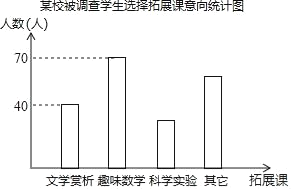
����Ŀ��Ϊ�ḻѧ���Ŀ������ijУ�ǻ���չ������չ�λ���ֱ��ǡ���ѧ����������Ȥζ��ѧ��������ѧʵ�顱����Ŀ��Ҫ��ÿλѧ������ѡ������һ����չ�βμӣ������ȡ��У����β���ѧ������ѡ����չ�ε�������е��ˣ�������Ľ������������ͳ��ͼ�Ͳ�������ͳ�Ʊ���
ijУ������ѧ��ѡ����չ������ͳ�Ʊ�
ѡ������ | ��ռ�ٷֱ� |
��ѧ���� | �� �� |
Ȥζ��ѧ | 35% |
��ѧʵ�� | �� �� |
���� | 30% |
��1����У��2000��ѧ����������ƴ�Լ�ж�����ѧ���μӿ�ѧʵ����չ�Σ�����ȫͳ�Ʊ���
��2����У�μӿ�ѧʵ����չ�ε�ѧ������ֳ�A��B��C����������ͬ�İ༶��С�ۺ�С�����μӿ�ѧʵ����չ�Σ�������ͬ�༶�ĸ��ʣ�����״ͼ���б�����⣩