题目内容
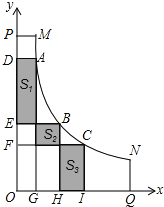
【题目】六一儿童节,小文到公园游玩.看到公园的一段人行弯道MN(不计宽度),如图,它与两面互相垂直的围墙OP、OQ之间有一块空地MPOQN(MP⊥OP,NQ⊥OQ),他发现弯道MN上任一点到两边围墙的垂线段与围墙所围成的矩形的面积都相等,比如:A、B、C是弯道MN上的三点,矩形ADOG、矩形BEOH、矩形CFOI的面积相等.爱好数学的他建立了平面直角坐标系(如图),图中三块阴影部分的面积分别记为S1、S2、S3,并测得S2=6(单位:平方米).OG=GH=HI.
(1)求S1和S3的值;
(2)设T(x,y)是弯道MN上的任一点,写出y关于x的函数关系式;
(3)公园准备对区域MPOQN内部进行绿化改造,在横坐标、纵坐标都是偶数的点处种植花木(区域边界上的点除外),已知MP=2米,NQ=3米.问一共能种植多少棵花木?
【答案】(1)![]() ;(2)
;(2)![]() ;(3)17.
;(3)17.
【解析】试题分析:(1)矩形ADOG、矩形BEOH、矩形CFOI的面积相等列方程组求解即可.
(2)由道MN上任一点到两边围墙的垂线段与围墙所围成的矩形的面积相等列式可得.
(3)把区域MPOQN内满足条件的点一一列出即可求解.
试题解析:解:(1)∵矩形ADOG、矩形BEOH、矩形CFOI的面积相等,且OG=GH=HI,
∴![]() .
.
又∵S2=6,∴![]() ,解得
,解得![]() .
.
(2)∵点T![]() 是弯道MN上的任一点,
是弯道MN上的任一点,
∴根据弯道MN上任一点到两边围墙的垂线段与围墙所围成的矩形的面积相等得![]() .
.
∴y关于x的函数关系式为![]() .
.
(3)∵MP=2,NQ=3,
∴当x=2时,y=18;当y=3时,x=12.
∵横坐标、纵坐标都是偶数,∴当x=4,6,8,10时,y=9,6, ![]() .
.
∴区域MPOQN内满足条件的点为(2,2),(2,4),(2,6),(2,8),(2,10),(2,12),(2,14),(2,16),(4,2),(4,4),(4,6),(4,8),(6,2),(6,4),(8,2),(8,4),(10,2),计17个.