��Ŀ����
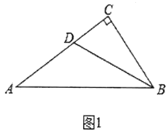
����Ŀ����ͼ1����֪������ABCD�ı߳�Ϊ1����E�ڱ�BC�ϣ�����AEF=900����EF����������ǵ�ƽ����CF�ڵ�F
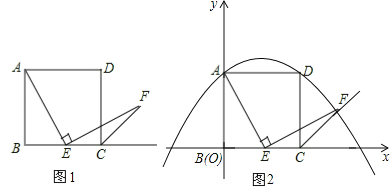
��1��ͼ1������E�DZ�BC���е㣬���ǿ��Թ�������������ȫ����֤��AE=EF�����������һ�����췽������ָ����������������ȫ�ȣ���Ҫ��֤������
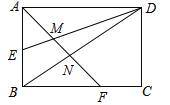
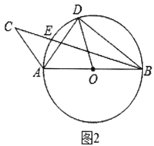
��2����ͼ2������E���߶�BC�ϻ����������B��C�غϣ���
��AE=EF�Ƿ��ܳ����������֤����
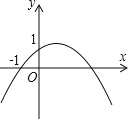
������ͼ2��ֱ������ϵ�У�����E������ij��ʱ����Fǡ������������![]() �ϣ����ʱ��F�����꣮
�ϣ����ʱ��F�����꣮
���𰸡���1����AGE����ECF��2����������![]()
��������
��1��ȡAB���е�G������EG������ASA�ܵõ���AGE����ECFȫ�ȣ�
��2������AB�Ͻ�ȡAG=EC����ASA֤����AGE�ա�ECF����֤��AE=EF��
������F��FH��x����H������FH=BE=CH��BH=a����FH=a��1��Ȼ���ʾ����F�����꣬���ݵ�Fǡ������������![]() �ϵõ��й�a�ķ������aֵ������õ�F�����꣮
�ϵõ��й�a�ķ������aֵ������õ�F�����꣮
�⣺��1����ͼ��ȡAB���е�G������EG������AGE����ECFȫ�ȣ�

��2��������E���߶�BC�ϻ���ʱAE=EF�ܳ�����֤�����£���ͼ��
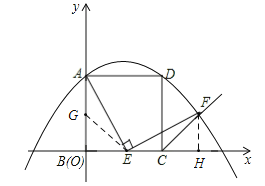
��AB�Ͻ�ȡAG=EC��
��AB=BC��
��BG=BE��
���GBE�ǵ���ֱ�������Σ�
���AGE=180����45��=135����
����CFƽ�������ε���ǣ�
���ECF=135����
���AGE=��ECF��
���ߡ�BAE+��AEB=��CEF+��AEB=90����
���BAE=��CEF��
���AGE�ա�ECF��ASA����
��AE=EF��
������F��FH��x����H��
����֪��FH=BE=CH����BH=a����FH=a��1��
����F������ΪF��a��a��1����
����Fǡ������������![]() �ϣ�
�ϣ�
��![]() ��
��
��a2=2����![]() ����ֵ�������⣬��ȥ����
����ֵ�������⣬��ȥ����
��![]() ������F������Ϊ
������F������Ϊ![]() ��
��