题目内容
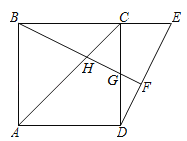
【题目】如图,点E是正方形ABCD的边BC延长线上一点,连结DE,过顶点B作BF⊥DE,垂足为F,BF分别交AC于H,交BC于G.
(1)求证:BG=DE;
(2)若点G为CD的中点,求![]() 的值.
的值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题分析:(1)由于BF⊥DE,所以∠GFD=90°,从而可知∠CBG=∠CDE,根据全等三角形的判定即可证明△BCG≌△DCE,从而可知BG=DE;
(2)设CG=1,从而知CG=CE=1,由勾股定理可知:DE=BG=![]() ,由易证△ABH∽△CGH,所以
,由易证△ABH∽△CGH,所以![]() =2,从而可求出HG的长度,进而求出
=2,从而可求出HG的长度,进而求出![]() 的值.
的值.
试题解析:(1)∵BF⊥DE,∴∠GFD=90°,∵∠BCG=90°,∠BGC=∠DGF,∴∠CBG=∠CDE,在△BCG与△DCE中,∵∠CBG=∠CDE,BC=CD,∠BCG=∠DCE,∴△BCG≌△DCE(ASA),∴BG=DE;
(2)设CG=1,∵G为CD的中点,∴GD=CG=1,由(1)可知:△BCG≌△DCE(ASA),∴CG=CE=1,∴由勾股定理可知:DE=BG=![]() ,∵sin∠CDE=
,∵sin∠CDE=![]() ,∴GF=
,∴GF=![]() ,∵AB∥CG,∴△ABH∽△CGH,∴
,∵AB∥CG,∴△ABH∽△CGH,∴![]() ,∴BH=
,∴BH=![]() ,GH=
,GH=![]() ,∴
,∴![]() =
=![]() .
.

练习册系列答案
相关题目