题目内容
【题目】如图,△ABC中,AB=AC,∠A=36°,D是AC上一点,且BD=BC,过点D分别作DE⊥AB,DF⊥BC,垂足分別是E,F,下列结论:①BD是∠ABC的平分线;②D是AC的中点;③DE垂直平分AB;④AB=BC+CD;其中正确的结论是_____(填序号).
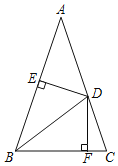
【答案】①③④
【解析】
根据等腰三角形的性质可得∠ABC=∠C=∠BDC=72°,利用外角性质可得∠ABD=36°,可得∠ABD=∠A=∠DBC=36°,根据等腰三角形的性质对各选项逐一判定即可得答案.
①∵∠A=36°,AB=AC,
∴∠ABC=∠C=72°,
∵BD=BC,
∴∠BDC=∠C=72°,
∵∠BDC=∠A+∠ABD,
∴∠ABD=36°,
∴∠ABD=∠CBD=36°,即BD是∠ABC的平分线,①正确.
②∵∠A+∠ABD=36°,
∴AD=BD,
∵BD≠CD,
∴AD≠CD,故②错误;
③∵∠ABD=∠A=36°,
∴AD=BD,
∵DE⊥AB,
∴AE=BE,
∴DE垂直平分AB,③正确;
④由①③可知,AD=BD=BC,
∵AB=AC,
∴AB=AD+CD=BC+CD,④正确;
综上所述,正确的结论有①③④,
故答案为:①③④.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】益马高速通车后,将桃江马迹塘的农产品运往益阳的运输成本大大降低。马迹塘一农户需要将A,B两种农产品定期运往益阳某加工厂,每次运输A,B产品的件数不变,原来每运一次的运费是1200元,现在每运一次的运费比原来减少了300元,A,B两种产品原来的运费和现在的运费(单位:元∕件)如下表所示:
品种 | A | B |
原来的运费 | 45 | 25 |
现在的运费 | 30 | 20 |
(1)求每次运输的农产品中A,B产品各有多少件?
(2)由于该农户诚实守信,产品质量好,加工厂决定提高该农户的供货量,每次运送的总件数增加8件,但总件数中B产品的件数不得超过A产品件数的2倍,问产品件数增加后,每次运费最少需要多少元?