题目内容
【题目】益马高速通车后,将桃江马迹塘的农产品运往益阳的运输成本大大降低。马迹塘一农户需要将A,B两种农产品定期运往益阳某加工厂,每次运输A,B产品的件数不变,原来每运一次的运费是1200元,现在每运一次的运费比原来减少了300元,A,B两种产品原来的运费和现在的运费(单位:元∕件)如下表所示:
品种 | A | B |
原来的运费 | 45 | 25 |
现在的运费 | 30 | 20 |
(1)求每次运输的农产品中A,B产品各有多少件?
(2)由于该农户诚实守信,产品质量好,加工厂决定提高该农户的供货量,每次运送的总件数增加8件,但总件数中B产品的件数不得超过A产品件数的2倍,问产品件数增加后,每次运费最少需要多少元?
【答案】(1)每次运输的农产品中A产品有10件,每次运输的农产品中B产品有30件,(2)产品件数增加后,每次运费最少需要850元.
【解析】
(1)设每次运输的农产品中A产品有x件,每次运输的农产品中B产品有y件,根据表中的数量关系列出关于x和y的二元一次方程组,解之即可,
(2)设增加m件A产品,则增加了(8-m)件B产品,设增加供货量后得运费为W元,根据(1)的结果结合图表列出W关于m的一次函数,再根据“总件数中B产品的件数不得超过A产品件数的2倍”,列出关于m的一元一次不等式,求出m的取值范围,再根据一次函数的增减性即可得到答案.
(1)设每次运输的农产品中A产品有x件,每次运输的农产品中B产品有y件,
根据题意得:
![]() ,
,
解得:![]() ,
,
答:每次运输的农产品中A产品有10件,每次运输的农产品中B产品有30件,
(2)设增加m件A产品,则增加了(8-m)件B产品,设增加供货量后得运费为W元,
增加供货量后A产品的数量为(10+m)件,B产品的数量为30+(8-m)=(38-m)件,
根据题意得:W=30(10+m)+20(38-m)=10m+790,
由题意得:38-m≤2(10+m),
解得:m≥6,
即6≤m≤8,
∵一次函数W随m的增大而增大
∴当m=6时,W最小=850,
答:产品件数增加后,每次运费最少需要850元.

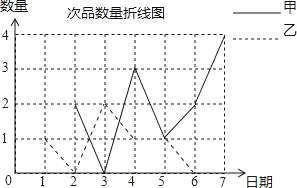
【题目】甲、乙两名工人同时加工同一种零件,现根据两人7天产品中每天出现的次品数情况绘制成如下不完整的统计图和表,依据图、表信息,解答下列问题:
相关统计量表:
量数 人 | 众数 | 中位数 | 平均数 | 方差 |
甲 |
|
| 2 |
|
乙 | 1 | 1 | 1 |
|
次品数量统计表:
天数 人 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
甲 | 2 | 2 | 0 | 3 | 1 | 2 | 4 |
乙 | 1 | 0 | 2 | 1 | 1 | 0 |
|
(1)补全图、表.
(2)判断谁出现次品的波动小.
(3)估计乙加工该种零件30天出现次品多少件?