题目内容
已知抛物线y=
x2-x-
(1)求该抛物线的对称轴和顶点坐标;
(2)求抛物线与x轴交点的坐标;
(3)画出抛物线的示意图;
(4)根据图象回答:当x在什么范围时,y随x的增大而增大?当x在什么范围时,y随x的增大而减小?
(5)根据图象回答:当x为何值时,y>0;当x为何值时,y<0.

| 1 |
| 2 |
| 3 |
| 2 |
(1)求该抛物线的对称轴和顶点坐标;
(2)求抛物线与x轴交点的坐标;
(3)画出抛物线的示意图;
(4)根据图象回答:当x在什么范围时,y随x的增大而增大?当x在什么范围时,y随x的增大而减小?
(5)根据图象回答:当x为何值时,y>0;当x为何值时,y<0.

(1)∵y=
x2-x-
=
(x2-2x+1-4)=
(x-1)2-2,
∴对称轴为x=1,顶点坐标为(1,-2);
(2)令y=
x2-x-
=0,
解得:x=-1或x=3,
∴图象与x轴的交点为(-1,0)和(3,0);
(3)图象为:
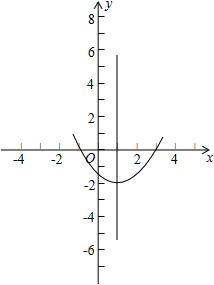
(4)当x>1时,y随x的增大而增大,当x<1时,y随x的增大而减小;
(5)当x<-1或x>3时,y>0;当-1<x<3时,y<0.
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴对称轴为x=1,顶点坐标为(1,-2);
(2)令y=
| 1 |
| 2 |
| 3 |
| 2 |
解得:x=-1或x=3,
∴图象与x轴的交点为(-1,0)和(3,0);
(3)图象为:
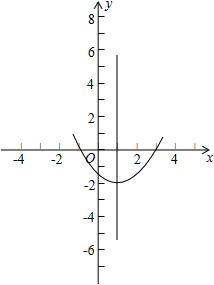
(4)当x>1时,y随x的增大而增大,当x<1时,y随x的增大而减小;
(5)当x<-1或x>3时,y>0;当-1<x<3时,y<0.

练习册系列答案
相关题目
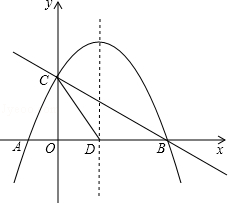
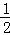 x2+mx+n与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(﹣1,0),C(0,2).
x2+mx+n与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(﹣1,0),C(0,2).