ЬтФПФкШн
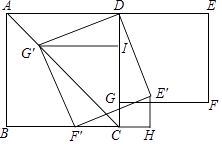
ЁОЬтФПЁПШчЭМЃЌдкRtЁїABCжаЃЌЁЯABC=90ЁуЃЎAB=BCЃЎЕуDЪЧЯпЖЮABЩЯЕФвЛЕуЃЌСЌНсCDЃЎЙ§ЕуBзїBGЁЭCDЃЌЗжБ№НЛCDЁЂCAгкЕуEЁЂFЃЌгыЙ§ЕуAЧвДЙжБгкABЕФжБЯпЯрНЛгкЕуGЃЌСЌНсDFЃЌИјГівдЯТЫФИіНсТлЃКЂй ![]() =
= ![]() ЃЛЂкШєЕуDЪЧABЕФжаЕуЃЌдђAF=
ЃЛЂкШєЕуDЪЧABЕФжаЕуЃЌдђAF= ![]() ABЃЛЂлЕБBЁЂCЁЂFЁЂDЫФЕудкЭЌвЛИідВЩЯЪБЃЌDF=DBЃЛЂмШє
ABЃЛЂлЕБBЁЂCЁЂFЁЂDЫФЕудкЭЌвЛИідВЩЯЪБЃЌDF=DBЃЛЂмШє ![]() =
= ![]() ЃЌдђSЁїABC=9SЁїBDF ЃЌ Цфжае§ШЗЕФНсТлађКХЪЧЃЈ ЃЉ
ЃЌдђSЁїABC=9SЁїBDF ЃЌ Цфжае§ШЗЕФНсТлађКХЪЧЃЈ ЃЉ
A.ЂйЂк
B.ЂлЂм
C.ЂйЂкЂл
D.ЂйЂкЂлЂм
ЁОД№АИЁПC
ЁОНтЮіЁПНтЃКвРЬтвтПЩЕУBCЁЮAGЃЌ
ЁрЁїAFGЁзЁїBFCЃЌ
Ёр ![]() ЃЌ
ЃЌ
гжAB=BCЃЌЁр ![]() ЃЎ
ЃЎ
ЙЪНсТлЂйе§ШЗЃЛ
ШчгвЭМЃЌЁпЁЯ1+ЁЯ3=90ЁуЃЌЁЯ1+ЁЯ4=90ЁуЃЌ
ЁрЁЯ3=ЁЯ4ЃЎ
дкЁїABGгыЁїBCDжаЃЌ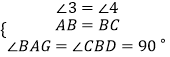 ЃЌ
ЃЌ
ЁрЁїABGЁеЁїBCDЃЈASAЃЉЃЌ
ЁрAG=BDЃЌгжBD=ADЃЌ
ЁрAG=ADЃЛ
дкЁїAFGгыЁїAFDжаЃЌ 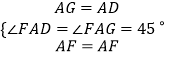 ЃЌ
ЃЌ
ЁрЁїAFGЁеЁїAFDЃЈSASЃЉ
ЁпЁїABCЮЊЕШбќжБНЧШ§НЧаЮЃЌЁрAC= ![]() ABЃЛ
ABЃЛ
ЁпЁїAFGЁеЁїAFDЃЌЁрAG=AD= ![]() AB=
AB= ![]() BCЃЛ
BCЃЛ
ЁпЁїAFGЁзЁїBFCЃЌЁр ![]() =
= ![]() ЃЌЁрFC=2AFЃЌ
ЃЌЁрFC=2AFЃЌ
ЁрAF= ![]() AC=
AC= ![]() ABЃЎ
ABЃЎ
ЙЪНсТлЂке§ШЗЃЛ
ЕБBЁЂCЁЂFЁЂDЫФЕудкЭЌвЛИідВЩЯЪБЃЌ
ЁрЁЯ2=ЁЯACB
ЁпЁЯABC=90ЁуЃЌAB=BCЃЌ
ЁрЁЯACB=ЁЯCAB=45ЁуЃЌ
ЁрЁЯ2=45ЁуЃЌ
ЁрЁЯCFD=ЁЯAFD=90ЁуЃЌ
ЁрCDЪЧBЁЂCЁЂFЁЂDЫФЕуЫљдкдВЕФжБОЖЃЌ
ЁпBGЁЭCDЃЌ
Ёр ![]() ЃЌ
ЃЌ
ЁрDF=DBЃЌЙЪЂле§ШЗЃЛ
Ёп ![]() ЃЌЁпAG=BDЃЌ
ЃЌЁпAG=BDЃЌ ![]() ЃЌ
ЃЌ
Ёр ![]() ЃЌЁр
ЃЌЁр ![]() =
= ![]() ЃЌЁрAF=
ЃЌЁрAF= ![]() ACЃЌЁрSЁїABF=
ACЃЌЁрSЁїABF= ![]() SЁїABCЃЛЁрSЁїBDF=
SЁїABCЃЛЁрSЁїBDF= ![]() SЁїABF ЃЌ
SЁїABF ЃЌ
ЁрSЁїBDF= ![]() SЁїABC ЃЌ МДSЁїABC=12SЁїBDF ЃЎ
SЁїABC ЃЌ МДSЁїABC=12SЁїBDF ЃЎ
ЙЪНсТлЂмДэЮѓЃЎ
ЙЪбЁCЃЎ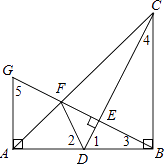
ЁОПМЕуОЋЮіЁПЙигкБОЬтПМВщЕФНтжБНЧШ§НЧаЮЃЌашвЊСЫНтНтжБНЧШ§НЧаЮЕФвРОнЃКЂйБпЕФЙиЯЕa2+b2=c2ЃЛЂкНЧЕФЙиЯЕЃКA+B=90ЁуЃЛЂлБпНЧЙиЯЕЃКШ§НЧКЏЕФЖЈвхЃЎ(зЂвтЃКОЁСПБмУтЪЙгУжаМфЪ§ОнКЭГ§ЗЈ)ВХФмЕУГіе§ШЗД№АИЃЎ

 ЯАЬтОЋбЁЯЕСаД№АИ
ЯАЬтОЋбЁЯЕСаД№АИЁОЬтФПЁПдкИеИеБеФЛЕФ2016ШЋЙњЁАСНЛсЁБЃЌУёЩњЛАЬтвРШЛЪЧЩчЛсНЙЕуЃЌФГЪаМЧепЮЊСЫСЫНтАйаеЖдЁАСНЛсУёЩњЛАЬтЁБЕФОлНЙЕуЃЌЫцЛњЕїВщСЫВПЗжЪаУёЃЌВЂЖдЕїВщНсЙћНјааећРэЃЎЛцжЦСЫШчЭМЫљЪОЕФЭГМЦЭМБэЃЈВЛЭъећЃЉЃЎ 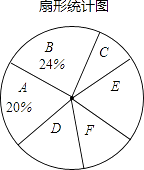
юlЪ§ЗжВМБэ
зщБ№ | НЙЕуЛАЬт | ЦЕЪ§ЃЈШЫЪ§ЃЉ |
A | вНСЦЮРЩњ | 100 |
B | ЪГЦЗАВШЋ | m |
C | НЬг§зЁЗП | 40 |
D | ЩчЛсБЃеЯ | 80 |
E | ЩњЬЌЛЗОГ | n |
F | ЦфЫћ | 60 |
ЧыИљОнЭМБэжаЬсЙЉЕФаХЯЂНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉЬюПеЃКm= ЃЌ n= ЃЎ ЩШаЮЭГМЦЭМжаEзщЃЌFзщЫљеМЕФАйЗжБШЗжБ№ЮЊЁЂ
ЃЈ2ЃЉИУЪаЯжгаШЫПкДѓдМ800ЭђЃЌЧыФуЙРМЦЦфжаЙизЂBзщЛАЬтЕФШЫЪ§ЃЛ
ЃЈ3ЃЉШєдкетДЮНгЪмЕїВщЕФЪаУёжаЃЌЫцЛњГщВщвЛШЫЃЌдђДЫШЫЙизЂAзщЛАЬтЕФИХТЪЪЧЖрЩйЃП