题目内容
【题目】如图，在△ABC中，∠C＝90°，∠A＝30°，BC＝1，点D在边AC上，且∠DBC＝45°，求sin∠ABD的值．
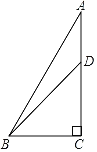
【答案】
【解析】
如图，作DM⊥AB于M，在BA上取一点H，使得BH＝DH，连接DH．设DM＝a．解直角三角形求出BD即可解决问题．
解：如图，过点D作DM⊥AB于M，在BA上取一点H，使得BH＝DH，连接DH．设DM＝a．
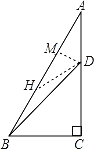
∵∠C＝90°，∠A＝30°，
∴∠ABC＝90°﹣30°＝60°，
∵∠DBC＝45°，
∴∠ABD＝60°﹣45°＝15°，
∵HB＝HD，
∴∠HBD＝∠HDB＝15°，
∴∠DHM＝∠HBD+∠HDB＝30°，
∴DH＝BH＝2a，MH＝
a，BM＝2a+a，
∴BD＝
，
∴sin∠ABD＝
．
练习册系列答案
相关题目
