Question

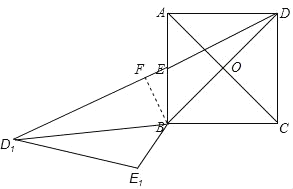
【题目】如图，正方形ABCD的边长为4，点O为对角线AC、BD的交点，点E为边AB的中点，△BED绕着点B旋转至△BD1E1，如果点D、E、D1在同一直线上，那么EE1的长为______．

Answer 1

【答案】

【解析】

根据正方形的性质得到AB＝AD＝4，根据勾股定理得到BD＝，DE＝，过B作BF⊥DD1于F，根据相似三角形的性质得到EF＝，求得DF＝，根据旋转的性质得到BD1＝BD，∠D1BD＝∠E1BE，BE1＝BE，根据相似三角形的性质即可得到结论．

解：∵正方形ABCD的边长为4，

∴AB＝AD＝4，

∴BD＝AB＝4，

∵点E为边AB的中点，

∴AE＝AB＝2，

∵∠EAD＝90°，

∴DE＝，

过B作BF⊥DD1于F，

∴∠DAE＝∠EFB＝90°，

∵∠AED＝∠BFE，

∴△ADE∽△FEB，

∴EF＝，

∴DF＝，

∵△BED绕着点B旋转至△BD1E1，

∴BD1＝BD，∠D1BD＝∠E1BE，BE1＝BE，

∴DD1＝2DF＝，△D1BD∽△E1BE，

∴，

∴，

∴EE1＝，

故答案为．