题目内容
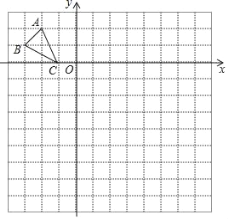
【题目】在平面直角坐标系xOy中,将抛物线y=﹣x2平移后经过点A(﹣1,0)、B(4,0),且平移后的抛物线与y轴交于点C(如图).
(1)求平移后的抛物线的表达式;
(2)如果点D在线段CB上,且CD=![]() ,求∠CAD的正弦值;
,求∠CAD的正弦值;
(3)点E在y轴上且位于点C的上方,点P在直线BC上,点Q在平移后的抛物线上,如果四边形ECPQ是菱形,求点Q的坐标.
【答案】(1)y=﹣x2+3x+4;(2)sin∠CAD=![]() ;(3)点Q的坐标为(4-
;(3)点Q的坐标为(4-![]() ,5
,5![]() -2).
-2).
【解析】
(1)根据平移前后a的值不变,用待定系数法求解即可;
(2)求出直线BC的解析式,确定点D的坐标,过点D作DM⊥AC,过点B作BN⊥AC,垂足分别为点M、N,运用面积法求出BN,再根据相似三角形的性质求出DM,根据直角三角函数求解即可;
(3)设点Q的坐标为(n,﹣n2+3n+4),如果四边形ECPQ是菱形,则n>0,PQ∥y轴,PQ=PC,点P的坐标为(n,﹣n+4),根据邻边相等列出方程即可求解.
(1)设平移后的抛物线的解析式为y=﹣x2+bx+c.
将A(﹣1,0)、B(4,0),代入得![]()
解得:![]()
所以,y=﹣x2+3x+4.
(2)如图1
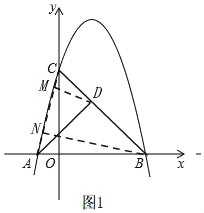
∵y=﹣x2+3x+4,∴点C的坐标为(0,4).
设直线BC的解析式为y=kx+4,将B(4,0),代入得kx+4=0,解得k=﹣1,
∴y=﹣x+4.
设点D的坐标为(m,4﹣m).
∵CD=![]() ,∴2=2m2,解得m=1或m=﹣1(舍去),
,∴2=2m2,解得m=1或m=﹣1(舍去),
∴点D的坐标为(1,3).
过点D作DM⊥AC,过点B作BN⊥AC,垂足分别为点M、N.
∵![]() ,
,
∴![]() ,
,
∴![]() .
.
∵DM∥BN,∴![]() ,
,
∴![]() ,
,
∴![]() .
.
∴![]() .
.
(3)如图2
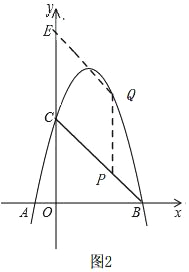
设点Q的坐标为(n,﹣n2+3n+4).
如果四边形ECPQ是菱形,则n>0,PQ∥y轴,PQ=PC,点P的坐标为(n,﹣n+4).
∵PQ=﹣n2+3n+4+n﹣4=4n﹣n2,![]() ,
,
∴![]() ,解得
,解得![]() 或n=0(舍).
或n=0(舍).
∴点Q的坐标为(![]() ,
,![]() ).
).

 导学教程高中新课标系列答案
导学教程高中新课标系列答案