题目内容
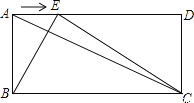
【题目】如图,在边长为 4 的等边△ABC 中,点 D 从点A 开始在射线 AB 上运动,速度为 1 个单位/秒,点F 同时从 C 出发,以相同的速度沿射线 BC 方向运动,过点D 作 DE⊥AC,连结 DF 交射线 AC 于点 G

(1)当 DF⊥AB 时,求 t 的值;
(2)当点 D 在线段 AB 上运动时,是否始终有 DG=GF?若成立,请说明理由。
(3)聪明的斯扬同学通过测量发现,当点 D 在线段 AB 上时,EG 的长始终等于 AC 的一半,他想当点D 运动到图 2 的情况时,EG 的长是否发生变化?若改变,说明理由;若不变,求出 EG 的长。
【答案】(1)![]() ;(2)见详解;(3)不变.
;(2)见详解;(3)不变.
【解析】
(1)设AD=x,则BD=4-x,BF=4+x.当DF⊥AB时,通过解直角△BDF求得x的值,易得t的值;
(2)如图1,过点D作DH∥BC交AC于点H,构建全等三角形:△DHG≌△FCG,结合全等三角形的对应边相等的性质和图中相关线段间的和差关系求得DG=GF;
(3)过F作FH⊥AC,可证△ADE≌△CFH,得DE=FH,AC=EH,再证△GDE≌△GFH,可得EG=GH,即可解题.
解:(1)设AD=x,则BD=4-x,BF=4+x.
当DF⊥AB时,∵∠B=60°,
∴∠DFB=30°,
∴BF=2BD,即4+x=2(4-x),
解得x=![]() ,
,
故t=![]() ;
;
(2)如图1,过点D作DH∥BC交AC于点H,则∠DHG=∠FCG.

∵△ABC是等边三角形,
∴△ADH是等边三角形,
∴AD=DH.
又AD=CF,
∴DH=FC.
∵在△DHG与△FCG中,
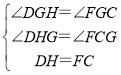 ,
,
∴△DHG≌△FCG(AAS),
∴DG=GF;
(3)如图2,过F作FH⊥AC,
在△ADE和△CFH中,
 ,
,
∴△ADE≌△CFH(AAS),
∴DE=FH,AE=CH,
∴AC=EH,
在△GDE和△GFH中,
 ∴△GDE≌△GFH(AAS),
∴△GDE≌△GFH(AAS),
∴EG=GH,
∴EG=![]() EH=
EH=![]() AC.
AC.