Question

【题目】（14分）如图，已知在矩形ABCD中，AB=a，BC=b，点E是线段AD边上的任意一点（不含端点A、D），连结BE、CE．

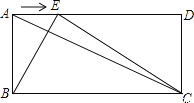
（1）若a=5，AC=13，求b．

（2）若a=5，b=10,当BE⊥AC时，求出此时AE的长．

（3）设AE=x，试探索点E在线段AD上运动过程中，使得△ABE与△BCE相似时，求a、b应满足什么条件，并求出此时x的值．

Answer 1

【答案】（1）b = 12 ；（2）；（3）

【解析】试题分析：（1）在矩形ABCD中，得到∠ABC=90°，利用勾股定理即可计算出结果.
（2）由∵BE⊥AC得到∠2+∠3=90°，由于∠1+∠3=90°，等量代换得到∠1=∠2，推出得到比例式，即可得到结论；
（3）点在线段上的任一点，且不与重合，当与相似时，则当（如图2），又由平行线的性质得到推出得到比例式，进而可得得到一元二次方程根据方程根的情况，得到结论．

试题解析：(1)∵四边形ABCD是矩形，

∵AB=a=5, AC=13，

∴b=12；

如图1，∵BE⊥AC

又

∴∠1 = ∠2,

又

∴△AEB ∽△BAC,

∴即,

∴.

（3）∵点E在线段AD上的任一点，且不与A、D重合，

∴当△ABE与△BCE相似时，则

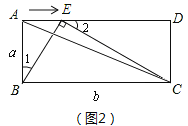
所以当△BAE ∽△CEB（如图2）

则∠1 = ∠BCE，

又BC∥AD,

∴∠2 = ∠BCE,

∴∠1 = ∠2 ,

又

∴△BAE ∽△EDC,

∴ 即 ,

∴ ,

即 ,

当 ,

∵a＞0，b＞0， ∴

即 时， .

综上所述：当a、b满足条件b = 2a时△BAE ∽△CEB，此时 (或x = a)；

当a、b满足条件b＞2a时△BAE ∽△CEB，此时.