ЬтФПФкШн
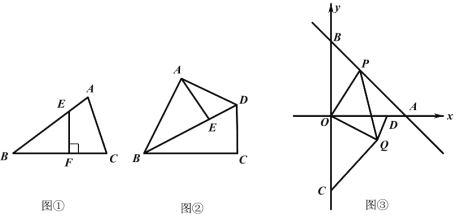
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌЕШБпШ§НЧаЮABCЕФЖЅЕуBгыдЕуOжиКЯЃЌЕуCдкxжсЩЯЃЌЕуCзјБъЮЊЃЈ6ЃЌ0ЃЉЃЌЕШБпШ§НЧаЮABCЕФШ§БпЩЯгаШ§ИіЖЏЕуDЁЂEЁЂFЃЈВЛПМТЧгыAЁЂBЁЂCжиКЯЃЉЃЌЕуDДгAЯђBдЫЖЏЃЌЕуEДгBЯђCдЫЖЏЃЌЕуFДгCЯђAдЫЖЏЃЌШ§ЕуЭЌЪБдЫЖЏЃЌЕНжеЕуНсЪјЃЌЧвЫйЖШОљЮЊ1cm/sЃЌЩшдЫЖЏЕФЪБМфЮЊtsЃЌНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉЧѓжЄЃКШчЭМЂйЃЌВЛТлtШчКЮБфЛЏЃЌЁїDEFЪМжеЮЊЕШБпШ§НЧаЮЃЎ
ЃЈ2ЃЉШчЭМЂкЙ§ЕуEзїEQЁЮABЃЌНЛACгкЕуQЃЌЩшЁїAEQЕФУцЛ§ЮЊSЃЌЧѓSгыtЕФКЏЪ§ЙиЯЕЪНМАtЮЊКЮжЕЪБЁїAEQЕФУцЛ§зюДѓЃПЧѓГіетИізюДѓжЕЃЎ
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌЕБЁїAEQЕФУцЛ§зюДѓЪБЃЌЦНУцФкЪЧЗёДцдквЛЕуPЃЌЪЙAЁЂDЁЂQЁЂPЙЙГЩЕФЫФБпаЮЪЧСтаЮЃЌШєДцдкЧыжБНгаДГіPзјБъЃЌШєВЛДцдкЧыЫЕУїРэгЩЃП

ЁОД№АИЁПЃЈ1ЃЉжЄУїМћНтЮіЃЛЃЈ2ЃЉЕБt=3ЪБЃЌЁїAEQЕФУцЛ§зюДѓЮЊ![]() cm2ЃЛЃЈ3ЃЉЃЈ3ЃЌ0ЃЉЛђЃЈ6ЃЌ3
cm2ЃЛЃЈ3ЃЉЃЈ3ЃЌ0ЃЉЛђЃЈ6ЃЌ3![]() ЃЉЛђЃЈ0ЃЌ3
ЃЉЛђЃЈ0ЃЌ3![]() ЃЉ
ЃЉ
ЁОНтЮіЁП
ЃЈ1ЃЉгЩШ§НЧаЮABCЮЊЕШБпШ§НЧаЮЃЌвдМАAD=BE=CFЃЌНјЖјЕУГіШ§НЧаЮADFгыШ§НЧаЮCFEгыШ§НЧаЮBEDШЋЕШЃЌРћгУШЋЕШШ§НЧаЮЖдгІБпЯрЕШЕУЕНBF=DF=DEЃЌМДПЩЕУжЄЃЛЃЈ2ЃЉЯШБэЪОГіШ§НЧаЮAECУцЛ§ЃЌИљОнEQгыABЦНааЃЌЕУЕНШ§НЧаЮCEQгыШ§НЧаЮABCЯрЫЦЃЌРћгУЯрЫЦШ§НЧаЮУцЛ§БШЕШгкЯрЫЦБШЕФЦНЗНБэЪОГіШ§НЧаЮCEQУцЛ§ЃЌНјЖјБэЪОГіAEQУцЛ§ЃЌРћгУЖўДЮКЏЪ§ЕФаджЪЧѓГіУцЛ§зюДѓжЕЃЌВЂЧѓГіДЫЪБQЕФзјБъМДПЩЃЛЃЈ3ЃЉЕБЁїAEQЕФУцЛ§зюДѓЪБЃЌDЁЂEЁЂFЖМЪЧжаЕуЃЌЗжСНжжЧщаЮЬжТлМД ПЩНтОіЮЪЬтЃЛ
ЃЈ1ЃЉШчЭМЂйжаЃЌ
ЁпCЃЈ6ЃЌ0ЃЉЃЌ
ЁрBC=6
дкЕШБпШ§НЧаЮABCжаЃЌAB=BC=AC=6ЃЌЁЯA=ЁЯB=ЁЯC=60ЁуЃЌ
гЩЬтвтжЊЃЌЕБ0ЃМtЃМ6ЪБЃЌAD=BE=CF=tЃЌ
ЁрBD=CE=AF=6ЉtЃЌ
ЁрЁїADFЁеЁїCFEЁеЁїBEDЃЈSASЃЉЃЌ
ЁрEF=DF=DEЃЌ
ЁрЁїDEFЪЧЕШБпШ§НЧаЮЃЌ
ЁрВЛТлtШчКЮБфЛЏЃЌЁїDEFЪМжеЮЊЕШБпШ§НЧаЮЃЛ

ЃЈ2ЃЉШчЭМЂкжаЃЌзїAHЁЭBCгкHЃЌдђAH=ABsin60Ёу=3![]() ЃЌ
ЃЌ

ЁрSЁїAEC=![]() ЁС3
ЁС3![]() ЁСЃЈ6ЉtЃЉ=
ЁСЃЈ6ЉtЃЉ=![]() ЃЌ
ЃЌ
ЁпEQЁЮABЃЌ
ЁрЁїCEQЁзЁїABCЃЌ
Ёр![]() =ЃЈ
=ЃЈ![]() ЃЉ2=
ЃЉ2=![]() ЃЌМДSЁїCEQ=
ЃЌМДSЁїCEQ=![]() SЁїABC=
SЁїABC=![]() ЁС9
ЁС9![]() =
=![]() ЃЌ
ЃЌ
ЁрSЁїAEQ=SЁїAECЉSЁїCEQ=![]() Љ
Љ![]() =Љ
=Љ![]() ЃЈtЉ3ЃЉ2+
ЃЈtЉ3ЃЉ2+![]() ЃЌ
ЃЌ
Ёпa=Љ![]() ЃМ0ЃЌ
ЃМ0ЃЌ
ЁрХзЮяЯпПЊПкЯђЯТЃЌгазюДѓжЕЃЌ
ЁрЕБt=3ЪБЃЌЁїAEQЕФУцЛ§зюДѓЮЊ![]() cm2ЃЌ
cm2ЃЌ
ЃЈ3ЃЉШчЭМЂлжаЃЌгЩЃЈ2ЃЉжЊЃЌEЕуЮЊBCЕФжаЕуЃЌЯпЖЮEQЮЊЁїABCЕФжаЮЛЯпЃЌ

ЕБADЮЊСтаЮЕФБпЪБЃЌПЩЕУP1ЃЈ3ЃЌ0ЃЉЃЌP3ЃЈ6ЃЌ3![]() ЃЉЃЌ
ЃЉЃЌ
ЕБADЮЊЖдНЧЯпЪБЃЌP2ЃЈ0ЃЌ3![]() ЃЉЃЌ
ЃЉЃЌ
злЩЯЫљЪіЃЌТњзуЬѕМўЕФЕуPзјБъЮЊЃЈ3ЃЌ0ЃЉЛђЃЈ6ЃЌ3![]() ЃЉЛђЃЈ0ЃЌ3
ЃЉЛђЃЈ0ЃЌ3![]() ЃЉЃЎ
ЃЉЃЎ

 УћаЃПЮЬУЯЕСаД№АИ
УћаЃПЮЬУЯЕСаД№АИ