Question

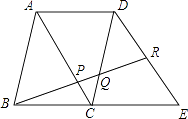
【题目】在△ABC中，∠B=60°，点P为BC边上一点，设BP=x，AP2=y（如图1），已知y是x的二次函数的一部分，其图象如图2所示，点Q（2，12）是图象上的最低点．

（1）边AB= ， BC边上的高AH=；
（2）当△ABP为直角三角形时，BP的长是多少．

Answer 1

【答案】
（1）4；2
（2）

解：当∠APB=90°时，在△ABP中，∠B=60°，

∴∠BAP=30°，∴BP= AB=2；

当∠BAP=90°时，在△ABP中，∠B=60°，

∴∠APB=30°，

∴BP=2AB=8．

综上可知当△ABP为直角三角形时，BP的长是2或8

【解析】解：（1）当AP⊥BC时可知AP2最小，
∵函数图象中过Q点时函数值最小，
∴AH= =2 ，即BC边上的高为2 ；
在Rt△ABH中，∠B=60°，
∴ =sin60°，即 = ，解得AB=4，
所以答案是：4；2 ；