��Ŀ����
����Ŀ�����壺����������y��ax2+bx+c��a��b��c�dz�����a��0������b2��ac����Ƹ�������Ϊ�ƽ������ߣ����磺y��2x2��2x+2�ǻƽ������ߣ�
��1������д��һ����������ͬ�Ļƽ������ߵĽ���ʽ��
��2����������y��ax2+bx+c��a��b��c�dz�����a��0���ǻƽ������ߣ���̽���ûƽ���������x��Ĺ���������������Ҫ��˵�����ɣ���
��3�����ƽ�������y��2x2��2x+2�ضԳ�������ƽ��3����λ��
��ֱ��д��ƽ�ƺ���������ߵĽ���ʽ��
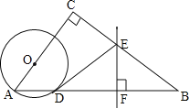
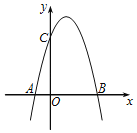
�������е�����������y�ύ�ڵ�A���Գ�����x�ύ�ڵ�B������Q�ڶԳ����ϣ��������������Ƿ���ڵ�P��ʹ�Ե�P��Q��BΪ��������������AOBȫ�ȣ������ڣ�ֱ��д�����з��������ĵ�P�����ꣻ�������ڣ���˵����
���𰸡���1����y��x2��y��x2��x+1��y��x2+2x+4�ȣ��𰸲�Ψһ������2�������������3����y��2x2��2x��1�������������ĵ�P�����꣺��0����1������1����1��������![]() ��
��![]() ������
������![]() ��
��![]() ����
����
��������
��1�����ջƽ������ߵĶ����a��b��c��ֵ���ɣ�
��2����ac��b2�����б�ʽ���У���ȥac��Ȼ���b�ֵ���0�Ͳ�����0���������ۼ��ɣ�
��3�������ݡ��ϼ��¼���д��ƽ�ƺ�������߽���ʽ���ɣ�
����������������������ֻ�ܻ�������ͼ�Σ��ֱ�д����Ӧ��P�����꼴�ɣ�
��1������y��x2��y��x2��x+1��y��x2+2x+4�ȣ�
��2���������b2��ac��
�����b2��4ac��b2��4b2����3b2��
�൱b��0ʱ������0����ʱ��������x����һ�������㣬
��b��0ʱ������0����ʱ��������x��û�й����㣻
��3��
��������y��2x2��2x+2����ƽ��3����λ�õ����������ߵĽ���ʽΪy��2x2��2x��1��
�����ڣ�
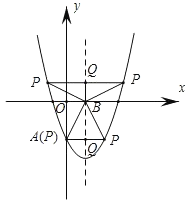
��ͼ��
��BQ��AO������Q��x���ƽ���ߣ����������ڵ�P��
P�����������0����1������1����1����
��ʱ����AOB�ա�BQP��
��BQ��BO������Q��x���ƽ���ߣ����������ڵ�P��
��2x2��2x��1��![]() ��
��
��ã�x����![]() ��x��
��x��![]() ��
��
��P�������������![]() ��
��![]() ������
������![]() ��
��![]() ����
����
��ʱ����AOB�ա�PQB��
�������������ĸ����������ĵ�P�����꣺��0����1������1����1��������![]() ��
��![]() ������
������![]() ��
��![]() ����
����

����Ŀ��ij��������Ӽס���������Ա��ѡȡһ����Ա�����öӲμӱ�������Ϊ�ס���������Ա������һ��ѡ������Ҫ����������Ա�����10��.�����������ݱ����ɼ���������ס���������Ա�ı����ɼ��Ƴ������µ�ͳ��ͼ(��)��
��Ա�ijɼ�ͳ�Ʊ�
�ɼ�(��λ����) | 7 | 8 | 9 | 10 |
����(�����) | 5 | 1 | 2 | 2 |
(1)��ͼ1�У�����8�����������ε�Բ�ĽǵĶ�����
(2)�����������õ��ķ����������������е�a��b��c��ֵ.
��Ա | ƽ���� | ��λ�� | ���� | ���� |
�� | 8 | 7.5 | 7 | c |
�� | a | b | 7 | 1 |
(3)���ݼס���������Ա�ijɼ���������������ѡ���Ҳμӱ���������д��һ�������ѡ���ҵ�����.