题目内容
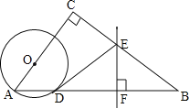
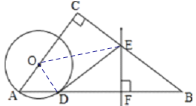
【题目】如图,在△ABC中,∠C=90°,点O在AC上,以OA为半径的⊙O交AB于点D,BD的垂直平分线交BC于点E,交BD于点F,连接DE.
(1)判断直线DE与⊙O的位置关系,并说明理由.
(2)若AC=3,BC=4,OA=1,求线段DE的长.
【答案】(1)相切,理由见解析;(2)![]() .
.
【解析】
(1)连接OD,根据圆的基本性质与垂直平分线的性质易得∠OAD=∠ODA,∠EDB=∠B,由∠OAD+∠B=90°,可得∠ODA+∠EDB=90°,即∠ODE=90°,根据切线的判定即可得解;
(2)连接OE,设DE=BE=x,则CE=8-x,在Rt△ODE与Rt△OCE中,利用勾股定理列出关于x的方程,然后求解方程即可.
解:(1)相切,理由如下:
如图,连接OD,
∵OA=OD,
∴∠OAD=∠ODA,
∵EF垂直平分BD,
∴DE=BE,
∴∠EDB=∠B,
∵∠C=90°,
∴∠OAD+∠B=90°,
∴∠ODA+∠EDB=90°,
∴∠ODE=90°,
∴直线DE与⊙O相切;
(2)连接OE,
设DE=BE=x,则CE=4﹣x,
∵AC=3, OA=1,
∴OC=2,
在Rt△ODE与Rt△OCE中,
OD2+DE2=CE2+OC2=OE2,
12+x2=(4﹣x)2+22,
解得x=![]() .
.

【题目】暑假到了,即将迎来手机市场的销售旺季.某商场销售甲、乙两种品牌的智能手机,这两种手机的进价和售价如下表所示:
甲 | 乙 | |
进价(元/部) | 4000 | 2500 |
售价(元/部) | 4300 | 3000 |
该商场计划投入15.5万元资金,全部用于购进两种手机若干部,期望全部销售后可获毛利润不低于2万元.(毛利润=(售价﹣进价)×销售量)
(1)若商场要想尽可能多的购进甲种手机,应该安排怎样的进货方案购进甲乙两种手机?
(2)通过市场调研,该商场决定在甲种手机购进最多的方案上,减少甲种手机的购进数量,增加乙种手机的购进数量.已知乙种手机增加的数量是甲种手机减少的数量的2倍,而且用于购进这两种手机的总资金不超过16万元,该商场怎样进货,使全部销售后获得的毛利润最大?并求出最大毛利润.